Eulerin kaava — määritelmä, e^{ix} ja yhteys trigonometriaan

Kompleksianalyysissä Eulerin kaava, jota joskus kutsutaan myös Eulerin suhteeksi, on yhtälö, joka yhdistää kompleksilukuja ja trigonometrisia funktioita. Tarkemmin sanottuna se sanoo, että

e i x = cos x + i sin x {\displaystyle e^{ix}=\cos x+i\sin x}

missä x on reaaliluku, e on Eulerin luku ja i on imaginääriyksikkö. Kaava muodostaa luonnollisen yhteyden trigonometrisen muodon ja kompleksilukujen eksponenttifunktion välillä. Se on nimetty Leonhard Eulerin mukaan, joka esitteli kaavan vuonna 1748.

Mitä Eulerin kaava kertoo

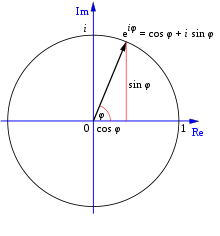
Eulerin kaava ilmaisee, että kompleksissa tasossa yksikköympyrän pisteet voidaan esittää eksponenttimuodossa: kulma x vastaa pistettä, jonka koordinaatit ovat cos x ja sin x. Tämän seurauksena monia trigonometristen funktioiden ominaisuuksia voi johtaa eksponenttifunktion ominaisuuksista.

Erityistapaukset ja Eulerin identiteetti

Kun kulma on π, saadaan hyvin tunnettu identiteetti:

— ensin merkitään π kuvan avulla: π

— ja periodin vuoksi myös 2π.

Soveltamalla Eulerin kaavaa saadaan

e i π = - 1 {\displaystyle e^{i\pi }=-1}

ja vastaavasti

e i 2 π = 1 {\displaystyle e^{i2\pi }=1}

Edellä oleva yhtälö e^{i\pi} = -1 yhdistää viisi matematiikan peruskäsitettä (1, 0, π, e ja i) yhteen eleganttiin lauseeseen, jota kutsutaan usein Eulerin identiteetiksi.

Todistuksia ja perusteluita

Eulerin kaavaa voi johtaa monella eri tavalla; muutama tavallinen lähestymistapa:

• Potenssisarjat: sekä e^z että cos z ja sin z voidaan määrittää Taylorin sarjoina ja sarjat yhtyvät kompleksitasolla, mikä antaa yhtälön suoraan.
• Differential equation -lähestymistapa: funktio f(x)=e^{ix} toteuttaa differentiaaliyhtälön f' = i f ja alkuarvon f(0)=1; sama differentiaaliyhtälö ja alkuarvo toteutuvat myös f(x)=cos x + i sin x, joten funktiot ovat samoja.
• Geometrinen/harmoninen analyysi: Eulerin kaava näkyy myös Fourier-analyysissä ja ratkaisuna ympyrän parametrisoinnille kompleksitasossa.

Yhteys trigonometriaan ja kompleksimuoto

Eulerin kaava antaa polaariesityksen vilkkaasti käytetylle muunnokselle: jokainen kompleksiluku z ≠ 0 voidaan esittää muodossa

z = r e^{iθ} = r(\cos θ + i\sin θ),

missä r = |z| on luvun itseisarvo ja θ on argumentti (kulma). Tämä esitys on erityisen kätevä kertolaskuissa ja potenssien ottamisessa, ja se johtaa suoraan de Moivren lauseeseen: (r e^{iθ})^n = r^n e^{inθ}.

Ominaisuuksia

• Eksponentin additiisuus: e^{i(x+y)} = e^{ix} e^{iy}, mikä vastaa trigonometrisia summa-kaavoja.
• Jaksoisuus: e^{i(x+2πk)} = e^{ix} kaikille kokonaisluvuille k, koska cos ja sin ovat 2π-periodisia.
• Laajennus kompleksikulmiin: kaava pätee myös, kun x korvataan kompleksisella z: e^{z} = e^{x+iy} = e^{x}(\cos y + i\sin y).

Sovelluksia

• Signaalinkäsittely ja Fourier-analyysi: kompleksieksponentit ovat perusyksiköitä taajuusjakaumassa.
• Fysiikka: aaltoliikkeiden ja kvanttifysiikan kompleksivaiheiden kuvaus perustuu usein e^{iθ}-muotoon.
• Insinööritieteet: pyörimisiä ja vaihdetta käsitellään helposti polaarimuodossa ja kompleksieksponentteina.
• Matematiikka: monimutkaisten funktioiden tutkimus, ratkaisut differentiaaliyhtälöihin ja kompleksinen potenssilaskenta hyödyntävät Eulerin kaavaa.

Yhteenveto

Eulerin kaava on keskeinen yhteys kompleksilukujen eksponenttifunktion ja trigonometrisen parametrisaation välillä. Se tarjoaa tehokkaan työkalun sekä teoreettiseen matemaattiseen päättelyyn että lukuisille sovellusalueille fysiikassa, tekniikassa ja insinööritieteissä.

Kysymyksiä ja vastauksia

K: Mikä on Eulerin kaava?

K: Kuka julkaisi Eulerin kaavan?

K: Toimiiko kaava, kun kulma ei ole reaaliluku?

K: Mitä tapahtuu, kun kulma on pii?

K: Mitä tapahtuu, kun kulma on 2pi?

K: Mitä "e" tarkoittaa tässä yhtälössä?

K: Mitä "i" tarkoittaa tässä yhtälössä?

Hae kirjaimella