Frekvenssijakauma tilastotieteessä: määritelmä, esimerkit ja laskenta
Tilastotieteessä frekvenssijakauma on luettelo arvoista, joita muuttuja saa otoksessa. Se on yleensä luettelo, joka on järjestetty määrän mukaan, ja siitä käy ilmi, kuinka monta kertaa kukin arvo esiintyy. Frekvenssijakauma antaa yksinkertaisen ja selkeän kuvan havaintojen jakautumisesta ja on perusta monille tilastollisille analyyseille sekä visualisoinneille.
Mitä frekvenssijakauma sisältää
Perusmuodossaan frekvenssijakauma sisältää:
- Absoluuttiset frekvenssit (fi): kuinka monta havaintoa kullakin arvoilla tai luokalla on.
- Relatiiviset frekvenssit (pi = fi / n): absoluuttisen frekvenssin osuus kokonaisotoksesta n.
- Kumulatiiviset frekvenssit (Fk): frekvenssien kertymä alusta tiettyyn arvoon saakka (absoluuttinen tai suhteellinen).
- Prosentit: relatiivinen frekvenssi kerrottuna sadalla, helpottaa lukujen tulkintaa.
Esimerkki: Likert-asteikko
Jos esimerkiksi 100 ihmistä arvioi viisiportaisella Likertin-asteikolla samaa mieltä -väitettä (1 = täysin samaa mieltä, 5 = täysin eri mieltä), frekvenssijakauma voi olla:
| Vastaus | Absoluuttinen frekvenssi (fi) | Relatiivinen frekvenssi (pi) | Prosentti |
|---|---|---|---|
| 1 | 20 | 0,20 | 20 % |
| 2 | 25 | 0,25 | 25 % |
| 3 | 30 | 0,30 | 30 % |
| 4 | 15 | 0,15 | 15 % |
| 5 | 10 | 0,10 | 10 % |
| Yhteensä | 100 | 1,00 | 100 % |
Ryhmitelty frekvenssijakauma (jatkuvat muuttujat)
Tässä yksinkertaisessa taulukossa on kaksi haittaa. Kun muuttuja voi saada jatkuvia arvoja diskreettisten arvojen sijaan tai kun mahdollisten arvojen määrä on liian suuri, taulukon rakentaminen yksittäisille arvoille on vaikeaa tai mahdotonta. Tällaisissa tapauksissa käytetään arvojen vaihteluväleihin perustuvaa, ryhmiteltyä frekvenssijakaumaa.
Esimerkiksi luokan oppilaiden pituudet voidaan ryhmitellä 10 cm luokkiin:
| Pituus (cm) | f (absol.) | Rel. frekvenssi | Kumulatiivinen f |
|---|---|---|---|
| 150–159 | 2 | 0,07 | 2 |
| 160–169 | 8 | 0,27 | 10 |
| 170–179 | 14 | 0,47 | 24 |
| 180–189 | 6 | 0,20 | 30 |
| Yhteensä | 30 | 1,00 | 30 |
Kuinka laskea frekvensseja — toimenpiteet
- Määritä otoksen koko n (havaintojen lukumäärä).
- Laske jokaisen yksittäisen arvon tai luokan absoluuttinen frekvenssi fi (havaintojen lukumäärä kyseisessä luokassa).
- Laske relatiivinen frekvenssi pi = fi / n ja prosentti = pi × 100.
- Laske kumulatiivinen frekvenssi Fk = Σ fi (kertymä järjestyksessä).
Ryhmittelyn suunnittelu ja luokkien valinta
- Luokkien lukumäärä ja leveys vaikuttavat jakauman muotoon: liian paljon luokkia aiheuttaa kohinaa, liian vähän hukkaa yksityiskohtia.
- Yleisiä ohjenuoria: Sturgesin kaava luokkien määrälle k ≈ 1 + 3,322 · log10(n) ja Freedman–Diaconis-sääntö luokan leveydelle h = 2 · IQR · n^(−1/3), jossa IQR on havaintojen interkvartiiliväli.
- Määrittele luokkien rajat siten, että havaintoja ei lasketa kahteen luokkaan (yksi tapa on tehdä luokat muotoon [alaluku, yläluku) paitsi viimeinen luokka sisältää molemmat rajat).
Visualisointi
- Diskreetit tai kategoriset muuttujat: pylväsdiagrammi (bar chart).
- Jatkuvat muuttujat: histogrammi (luokat esitetään pylväinä, joiden ala kuvaa frekvenssiä), frekvenssifunktio tai frekvenssikolmio (frequency polygon).
- Kumulatiivisten frekvenssien visualisointi: ogive (kumulatiivinen käyrä) antaa nopeasti näkymän esimerkiksi mediaanin ja kvantiilien sijaintiin.
Esimerkkejä ohjelmistoissa
- Excel: käytä Pivot-taulukkoa tai COUNTIFS/COUNTIF-funktioita; histogrammi löytyy myös valmiina kaaviona.
- R: table(x) diskreetille muuttujalle; hist(x, breaks=...) ja cut(x, breaks=...) ryhmiteltäessä.
- Python (pandas): df['kol'].value_counts() diskreetille; pd.cut(df['kol'], bins=...) ja df.groupby(...) ryhmittelyyn; matplotlib/Seaborn histogrammeihin.
Hyödyt ja rajoitukset
- Frekvenssijakauma on helposti tulkittava ja antaa nopean yleiskuvan havainnoista.
- Ryhmittelyssä osa tiedosta häviää: tarkat arvot eivät ole näkyvissä luokkien sisällä, mikä voi peittää pienet mutta merkittävät yksityiskohdat.
- Luokkavalinnat ja otoskoko vaikuttavat vahvasti tulkintaan; siksi on tärkeää dokumentoida käytetyt luokat ja laskentatavat.
Yhteenveto
Frekvenssijakauma on perusväline tilastotieteessä: se kertoo, miten usein eri arvot esiintyvät otoksessa ja muodostaa pohjan suhteellisille frekvensseille, kumulatiivisille jakaumille ja visuaalisille esityksille kuten histogrammeille. Oikein suunniteltuna ja tulkittuna frekvenssijakauma auttaa ymmärtämään aineiston rakennetta ja löytämään mahdolliset poikkeamat tai mallit.
Tämä on Kiinan väestöpyramidi vuodelta 2005.
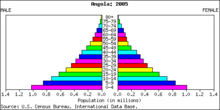
Esimerkki (absoluuttisesta) taajuusjakaumasta. Tämä on Angolan väestöpyramidi vuodelta 2005.
Sovellukset
Taajuusluokiteltujen tietojen hallinta ja käyttö on paljon yksinkertaisempaa kuin raakatietojen käyttö. Näistä taulukoista voidaan laskea yksinkertaisilla algoritmeilla mediaani, keskiarvo (tilastot), keskihajonta jne.
Tilastollinen hypoteesien testaus perustuu taajuusjakaumien välisten erojen ja yhtäläisyyksien arviointiin. Tähän arviointiin sisältyy keskitendenssin tai keskiarvojen mittauksia, kuten keskiarvo ja mediaani, ja vaihtelun tai tilastollisen hajonnan mittauksia, kuten keskihajonta tai varianssi.
Frekvenssijakauman sanotaan olevan vino, kun sen keskiarvo ja mediaani ovat erilaiset. Frekvenssijakauman kurtoosi on pistemäärien keskittyminen keskiarvon kohdalle tai se, kuinka huipulta jakauma näyttää, jos sitä kuvataan graafisesti - esimerkiksi histogrammissa. Jos jakauma on enemmän piikkinen kuin normaalijakauma, sen sanotaan olevan leptokurttinen; jos se on vähemmän piikkinen, sen sanotaan olevan platykurttinen.
Taajuusjakaumia käytetään myös taajuusanalyysissä koodien murtamiseen, ja niillä tarkoitetaan kirjainten suhteellista esiintymistiheyttä eri kielissä.
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Kysymyksiä ja vastauksia
Q: Mikä on taajuusjakauma?
A: Taajuusjakauma on luettelo muuttujan otoksessa ottamista arvoista, jotka on järjestetty määrän mukaan. Se osoittaa, kuinka monta kertaa kukin arvo esiintyy.
K: Miltä viisiportaisen Likert-asteikon vastausten frekvenssijakauma voisi näyttää?
V: Viisiportaisen Likert-asteikon vastausten frekvenssijakauma voi näyttää yksinkertaiselta taulukolta, josta käy ilmi, kuinka monta ihmistä arvioi kutakin asteikon kohtaa.
K: Mitkä ovat kaksi haittaa tämäntyyppisen taulukon käyttämisessä?
V: Kaksi haittapuolta tämäntyyppisen taulukon käytössä on se, että se voi olla vaikeaa tai jopa mahdotonta, kun kyseessä ovat jatkuvat arvot tai kun mahdollisia arvoja on liian monta.
K: Miten tämä järjestelmä eroaa, kun käsitellään jatkuvia arvoja tai suurta määrää mahdollisia arvoja?
V: Kun kyseessä ovat jatkuvat arvot tai suuri määrä mahdollisia arvoja, voidaan sen sijaan käyttää hieman erilaista arvojen vaihteluväliin perustuvaa järjestelmää.
K: Miltä opiskelijoiden pituuksia koskeva frekvenssitaulukko voisi näyttää?
V: Opiskelijoiden pituuksien frekvenssitaulukosta voisi käydä ilmi vaihteluvälit ja se, kuinka monta opiskelijaa kuuluu kuhunkin vaihteluväliin.
Kysymys: Mitä tietoa frekvenssijakauma antaa?
V: Frekvenssijakauma antaa tietoa siitä, kuinka usein tietyt muuttujat esiintyvät otoksissa ja miten ne jakautuvat näissä otoksissa.
