Ampèren kiertokulkulaki

Alkuperäinen Ampèren kiertolaki

Laki liittää magneettikentät niitä tuottaviin sähkövirtoihin. Tutkija voi käyttää Amperen lakia määrittääkseen tiettyyn virtaan liittyvän magneettikentän tai tiettyyn magneettikenttään liittyvän virran, jos ajassa muuttuvaa sähkökenttää ei ole. Alkuperäisessä muodossaan Ampèren kiertolaki liittää magneettikentän sen sähkövirran lähteeseen. Laki voidaan kirjoittaa kahdessa muodossa, "integraalimuodossa" ja "differentiaalimuodossa". Nämä muodot ovat ekvivalentteja ja liittyvät toisiinsa Kelvin-Stokesin lauseen avulla. Se voidaan myös kirjoittaa joko B- tai H-magneettikentän muodossa. Myös nämä kaksi muotoa ovat ekvivalentteja (ks. jäljempänä oleva "todiste"-osio).

Ampèren kiertolain tiedetään nyt olevan oikea fysiikan laki magnetostaattisessa tilanteessa: Järjestelmä on staattinen lukuun ottamatta mahdollisesti jatkuvia tasaisia virtoja suljetuissa silmukoissa. Kaikissa muissa tapauksissa laki on virheellinen, ellei Maxwellin korjausta oteta huomioon (ks. jäljempänä).

Integraalimuoto

SI-yksiköissä (versio cgs-yksiköissä on myöhemmässä jaksossa) alkuperäisen Ampèren kiertolain "integraalimuoto" on:

• ∮ C B ⋅ d ℓ = μ 0 ∬ S J ⋅ d S {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} }
• ∮ C H ⋅ d ℓ = ∬ S J f ⋅ d S {\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\mathbf {J} _{\\mathrm {f} \cdot \mathrm {d} \mathbf {S} }

tai vastaavasti,

• ∮ C B ⋅ d ℓ = μ 0 I e n c {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I_{\mathrm {enc} }}
• ∮ C H ⋅ d ℓ = I f , e n c {\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=I_{\mathrm {f,enc} }}

jossa

• - on vektorin pistetuotto, ∮ C {\displaystyle \textstyle \point _{C}} on suljettu viivaintegraali suljetun käyrän C ympärillä, ∬ S {\displaystyle \textstyle \iint _{S}} tarkoittaa integraalia käyrän C ympäröimän pinnan S yli (kaksoisintegraalin merkin tarkoituksena on vain ilmaista, että integraali on luonteeltaan kaksiulotteinen);
• B on magneettinen B-kenttä teslaina, H on magneettinen H-kenttä ampeereina metriä kohti;
• I_f,enc on pinnan S läpi kulkeva vapaa nettovirta, I_enc on pinnan S läpi kulkeva kokonaisnettovirta, joka sisältää sekä vapaan että sidotun virran.
• J_f on vapaan virran tiheys käyrän C ympäröimän pinnan S läpi, J on kokonaisvirran tiheys käyrän C ympäröimän pinnan S läpi, mukaan lukien sekä vapaa että sidottu virta;
• dℓ on käyrän C infinitesimaalinen elementti (differentiaali) (eli vektori, jonka suuruus on yhtä suuri kuin infinitesimaalisen suoran elementin pituus ja jonka suunnan antaa käyrän C tangentti), dS on pinnan S infinitesimaalisen elementin pinta-alan vektori (eli vektori, jonka suuruus on yhtä suuri kuin infinitesimaalisen pinta-alan elementin pinta-ala ja jonka suunta on normaali pintaan S nähden. Normaalin suunnan on vastattava oikean käden säännön mukaisesti C:n orientaatiota);
• μ₀ on magneettinen vakio;

Käyrää C ja pintaa S selitetään tarkemmin jäljempänä. Edellä olevissa määritelmissä on useita epäselvyyksiä, jotka edellyttävät selvennystä ja yleissopimuksen valintaa.

Ensinnäkin kolmeen näistä termeistä liittyy merkkien epäselvyyksiä: viivaintegraali ∮ C {\displaystyle \textstyle \textstyle \oint _{C}} voisi kiertää silmukan molempiin suuntiin (myötä- tai vastapäivään); vektoripinta-ala dS voisi osoittaa jompaankumpaan kahdesta suunnasta, jotka ovat normaaleja pintaan nähden; ja I_enc on pinnan S läpi kulkeva nettovirta, joka tarkoittaa yhdessä suunnassa kulkevaa virtaa vähennettynä virralla toisessa suunnassa - mutta kumpi tahansa suunta voitaisiin valita positiiviseksi. Nämä epäselvyydet ratkaistaan oikean käden säännön avulla: Oikean käden kämmenen ollessa kohti integrointialuetta ja etusormen osoittaessa viivaintegraation suuntaa, ojennettu peukalo osoittaa suuntaan, joka on valittava vektorin pinta-alalle dS. Myös virta, joka kulkee samaan suuntaan kuin dS, on laskettava positiiviseksi. Oikean käden otesääntöä voidaan käyttää myös merkkien määrittämiseen.

Toiseksi on äärettömän monta mahdollista pintaa S, joiden rajana on käyrä C. (Kuvittele saippuakalvo lankasilmukan päällä, jota voidaan muotoilla siirtämällä lankaa). Mikä näistä pinnoista valitaan? Jos silmukka ei esimerkiksi sijaitse yhdessä tasossa, ei ole olemassa yhtä selvää vaihtoehtoa. Vastaus on, että sillä ei ole väliä; voidaan osoittaa, että mikä tahansa pinta, jolla on raja C, voidaan valita.

Differentiaalimuoto

Kelvin-Stokesin lauseen mukaan tämä yhtälö voidaan kirjoittaa myös "differentiaalimuodossa". Tämäkin yhtälö pätee vain siinä tapauksessa, että sähkökenttä on vakio ajassa; katso jäljempänä yleisempi muoto. SI-yksiköissä yhtälö kuuluu seuraavasti:

∇ × B = μ 0 J \displaystyle \mathbf \nabla } \times \mathbf {B} =\mu _{0}\mathbf {J} }

∇ × H = J f \displaystyle \mathbf \nabla } \times \mathbf {H} =\mathbf {J_{f}} }

jossa

∇ × \displaystyle \mathbf \nabla } \times \!\ } on curl-operaattori.  

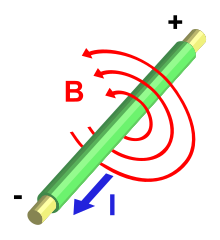
Sähkövirta tuottaa magneettikentän.  

Huomautus vapaasta virrasta ja sidotusta virrasta

Sähkövirta, joka syntyy yksinkertaisimmissa oppikirjatilanteissa, luokitellaan "vapaaksi virraksi". Lakia voidaan soveltaa esimerkiksi johtimen tai pariston läpi kulkevaan virtaan. Sitä vastoin "sidottu virta" syntyy irtotavaramateriaalien yhteydessä, jotka voidaan magnetoida ja/tai polarisoida. (Kaikki materiaalit voivat jossain määrin.)

Kun materiaali magnetoidaan (esimerkiksi asettamalla se ulkoiseen magneettikenttään), elektronit pysyvät sidottuina omiin atomeihinsa, mutta käyttäytyvät ikään kuin ne kiertäisivät ydintä tietyssä suunnassa, jolloin syntyy mikroskooppinen virta. Kun kaikkien näiden atomien virrat lasketaan yhteen, ne luovat saman vaikutuksen kuin makroskooppinen virta, joka kiertää jatkuvasti magnetoidun kappaleen ympärillä. Tämä magnetointivirta J_M on yksi osa "sidottua virtaa".

Toinen sidotun virran lähde on sidottu varaus. Kun sähkökenttää käytetään, positiiviset ja negatiiviset sidotut varaukset voivat erota toisistaan atomien etäisyyksillä polarisoituvissa materiaaleissa, ja kun sidotut varaukset liikkuvat, polarisaatio muuttuu, jolloin syntyy toinen osuus "sidotusta virrasta", polarisaatiovirta J_P .

Vapaiden ja sidottujen varausten aiheuttama kokonaisvirrantiheys J on tällöin:

J = J f + J M + J P , {\displaystyle \mathbf {J} =\mathbf {J_{f}+J_{M}+J_{P}}} \ ,}

J_f on "vapaa" tai "johtava" virrantiheys.

Mikroskooppisesti kaikki virta on pohjimmiltaan samanlaista. Usein on olemassa käytännön syitä, joiden vuoksi sidottua virtaa halutaan käsitellä eri tavalla kuin vapaata virtaa. Esimerkiksi sidottu virta syntyy yleensä atomiulottuvuuksissa, ja voidaan haluta hyödyntää yksinkertaisempaa teoriaa, joka on tarkoitettu suuremmille ulottuvuuksille. Tästä seuraa, että mikroskooppisempi Ampèren laki, joka ilmaistaan B:n ja mikroskooppisen virran (joka sisältää vapaan, magnetoitumis- ja polarisaatiovirran) suhteen, asetetaan joskus alla olevaan vastaavaan muotoon vain H:n ja vapaan virran suhteen. Vapaan virran ja sidotun virran yksityiskohtainen määritelmä ja todiste siitä, että nämä kaksi muotoilua ovat ekvivalentteja, on jäljempänä kohdassa "todiste".

 

Ampèren kiertolain alkuperäisen muotoilun puutteet

Ampèren lakiin liittyy kaksi tärkeää asiaa. Ensinnäkin on kysymys sähkövarauksen jatkuvuusyhtälöstä. Vektorilaskennassa on lause, jonka mukaan käyrän divergenssin on aina oltava nolla. Näin ollen

∇ ⋅ ( ∇ × B ) = 0 {\displaystyle \nabla \cdot (\nabla \times {\mathbf {B}})=0}

joten alkuperäinen Ampèren laki merkitsee, että

∇ ⋅ J = 0 {\displaystyle \nabla \cdot {\mathbf {J}}=0}

Mutta yleisesti ottaen

∇ ⋅ J = - ∂ ρ ∂ t {\displaystyle \nabla \cdot {\mathbf {J}}=-{\frac {\partial \rho }{\partial t}}}

joka on nollasta poikkeava, kun varaustiheys vaihtelee ajassa. Esimerkki tästä on kondensaattoripiiri, jossa levyjen varaustiheydet vaihtelevat ajassa.

Toiseksi on kysymys sähkömagneettisten aaltojen etenemisestä. Esimerkiksi vapaassa avaruudessa, jossa

J = 0 {\displaystyle {\mathbf {J}}={\mathbf {0}}}

Ampèren lain mukaan

∇ × B = 0 {\displaystyle \nabla \times {\mathbf {B}}={\mathbf {0}}}

vaan sen sijaan

∇ × B = - 1 c 2 ∂ E ∂ t {\displaystyle \nabla \times {\mathbf {B}}=-{\frac {1}{c^{2}}}{\frac {\partial {\mathbf {E}}}{\partial t}}}}

Näiden tilanteiden käsittelemiseksi Ampèren lain virran termiin on lisättävä siirtymävirran osuus.

James Clerk Maxwell käsitteli siirtymävirran polarisaatiovirraksi dielektrisessä pyörremeressä, jota hän käytti mallintamaan magneettikenttää vedellä (hydrodynaamisesti) ja mekaanisilla järjestelmillä (mekaanisesti). Hän lisäsi tämän siirtymävirran Ampèren kiertokulkulakiin yhtälössä (112) vuonna 1861 julkaistussa artikkelissaan On Physical Lines of Force .

Siirtymävirta

Vapaassa tilassa siirtymävirta liittyy sähkökentän muutosnopeuteen.

Myös dielektrisessä aineessa on edellä mainittu vaikutus siirtymävirtaan, mutta suurin vaikutus siirtymävirtaan liittyy dielektrisen aineen yksittäisten molekyylien polarisaatioon. Vaikka varaukset eivät voi virrata vapaasti dielektrisessä aineessa, molekyylien varaukset voivat liikkua hieman sähkökentän vaikutuksesta. Molekyylien positiiviset ja negatiiviset varaukset erkanevat toisistaan sovelletun kentän vaikutuksesta, mikä aiheuttaa polarisaatiotilan kasvun, joka ilmaistaan polarisaatiotiheytenä P. Muuttuva polarisaatiotila vastaa virtaa.

Molemmat siirtymävirran osuudet yhdistetään määrittelemällä siirtymävirta seuraavasti:

J D = ∂ ∂ t D ( r , t ) , {\displaystyle \mathbf {J_{D}} ={\frac {\partial }{\partial t}}\mathbf {D} ({\boldsymbol {r}},\ t)\ ,}

jossa sähköinen siirtymäkenttä määritellään seuraavasti:

D = ε 0 E + P = ε 0 ε r E , {\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} =\varepsilon _{0}\varepsilon _{r}\mathbf {E} \ ,}

jossa ε₀ on sähkövakio, ε_r on suhteellinen staattinen permittiivisyys ja P on polarisaatiotiheys. Kun tämä muoto korvataan D:llä siirtymävirran lausekkeeseen, sillä on kaksi komponenttia:

J D = ε 0 ∂ E ∂ t + ∂ P ∂ t . {\displaystyle \mathbf {J} _{\mathrm {D} }=\varepsilon _{0}{\frac {\partial \mathbf {E} {{\partial t}}+{\frac {\partial \mathbf {P}} }{\partial t}}. }

Oikeanpuoleinen ensimmäinen termi esiintyy kaikkialla, jopa tyhjiössä. Siihen ei liity varsinaista varauksen liikettä, mutta siihen liittyy kuitenkin magneettikenttä, aivan kuin se olisi varsinainen virta. Jotkut kirjoittajat käyttävät nimitystä siirtovirta vain tästä osuudesta.

Oikeanpuoleinen toinen termi on Maxwellin alun perin hahmottama siirtymävirta, joka liittyy dielektrisen materiaalin yksittäisten molekyylien polarisaatioon.

Maxwellin alkuperäinen selitys siirtymävirralle keskittyi dielektrisissä väliaineissa esiintyvään tilanteeseen. Nykyaikana, eetterin jälkeisenä aikakautena, käsitettä on laajennettu koskemaan myös tilanteita, joissa ei ole aineellista väliaineistoa, esimerkiksi tyhjiötä varaavan tyhjiökondensaattorin levyjen välissä. Siirtovirta on nykyään perusteltu, koska se palvelee useita sähkömagneettiselle teorialle asetettuja vaatimuksia: magneettikenttien oikea ennustaminen alueilla, joilla ei kulje vapaata virtaa; sähkömagneettisten kenttien aaltojen etenemisen ennustaminen; ja sähkövarauksen säilyminen tapauksissa, joissa varaustiheys on ajassa muuttuva. Tarkempi keskustelu on kohdassa Siirtymävirta.

 

Alkuperäisen lain laajentaminen: Maxwell-Ampèren yhtälö

Ampèren yhtälöä laajennettiin sisällyttämällä siihen polarisaatiovirta, jolloin alkuperäisen Ampèren kiertolain rajallinen sovellettavuus korjaantui.

Kun vapaita varauksia käsitellään erillään sidotuista varauksista, Ampèren yhtälö, joka sisältää Maxwellin korjauksen H-kentän suhteen, on (H-kenttää käytetään, koska se sisältää magnetointivirrat, joten J_M ei esiinny eksplisiittisesti, katso H-kenttä ja myös Huomautus):

∮ C H ⋅ d ℓ = ∬ S ( J f + ∂ ∂ t D ) ⋅ d A {\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\left(\mathbf {J} _{\\mathrm {f} }+{\frac {\partial t}}\mathbf {D}\mathbf {D} \right)\cdot \mathrm {d} \mathbf {A} }

(integraalimuoto), jossa H on magneettinen H-kenttä (jota kutsutaan myös "apumagneettikentäksi", "magneettikentän voimakkuudeksi" tai vain "magneettikentäksi", D on sähköinen siirtymäkenttä ja J_f on suljettu johtovirta tai vapaan virran tiheys. Differentiaalimuodossa,

∇ × H = J f + ∂ ∂ t D . {\displaystyle \mathbf {\nabla } \times \mathbf {H} =\mathbf {J} _{\mathrm {f} }+{\frac {\partial }{\partial t}}\mathbf {D}\mathbf {D} \ . }

Toisaalta, kun kaikkia varauksia kohdellaan samoin perustein (riippumatta siitä, ovatko ne sidottuja vai vapaita varauksia), yleistetty Ampèren yhtälö (jota kutsutaan myös Maxwell-Ampèren yhtälöksi) on (ks. "todiste" jäljempänä):

∮ C B ⋅ d ℓ = ∬ S ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) ⋅ d A {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\left(\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E}\mathbf {E} \right)\cdot \mathrm {d} \mathbf {A} }

integraalimuodossa. Differentiaalimuodossa,

∇ × B = ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) . {\displaystyle \mathbf {\nabla } \times \mathbf {B} =(\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}} \mathbf {E} \mathbf {E} )\ . }

Molemmissa muodoissa J sisältää magnetointivirran tiheyden sekä johtumis- ja polarisaatiovirran tiheydet. Toisin sanoen Ampère-Maxwellin yhtälön oikealla puolella oleva virrantiheys on:

J f + J D + J M = J f + J P + J M + ε 0 ∂ E ∂ t = J + ε 0 ∂ E ∂ t , {\displaystyle \mathbf {J_{f}+J_{D}+J_{M}} =\mathbf {J_{f}+J_{P}+J_{M}}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}=\mathbf {J}} +\varepsilon _{0}{\frac {\partial \mathbf {E} {{\partial t}}\ ,}\ ,}

jossa virrantiheys J_D on siirtymävirta ja J on virrantiheyden osuus, joka johtuu sekä vapaiden että sidottujen varausten liikkeestä. Koska ∇ - D = ρ, Ampèren alkuperäisen muotoilun varausjatkuvuusongelma ei ole enää ongelma. Koska termi ε₀ ∂E / ∂t, aaltojen eteneminen vapaassa tilassa on nyt mahdollista.

Siirtymävirran lisäämisen myötä Maxwell pystyi (oikein) päättelemään, että valo oli eräänlainen sähkömagneettinen aalto. Katso sähkömagneettisen aallon yhtälö, jossa käsitellään tätä tärkeää löytöä.

Vastaavuuden osoittaminen

Todiste siitä, että Ampèren lain ilmaisut vapaan virran muodossa vastaavat ilmaisuja, joissa on kyse kokonaisvirrasta.

Tässä todistuksessa osoitetaan, että yhtälö ∇ × H = J f + ∂ D ∂ t {\displaystyle \nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}} vastaa yhtälöä ∇ × B / μ 0 = J + ϵ 0 ∂ E ∂ t \displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {J} +\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}} Huomaa, että käsittelemme vain differentiaalimuotoja, emme integraalimuotoja, mutta se riittää, koska differentiaali- ja integraalimuodot ovat Kelvin-Stokesin lauseen mukaan kussakin tapauksessa ekvivalentteja. Otamme käyttöön polarisaatiotiheyden P, jolla on seuraava suhde E:hen ja D:hen: D = ϵ 0 E + P {\displaystyle \mathbf {D} =\epsilon _{0}\mathbf {E} +\mathbf {P} } Seuraavaksi esitellään magnetointitiheys M, jolla on seuraava suhde B:hen ja H:hen: B / μ 0 = H + M {\displaystyle \mathbf {B} /\mu _{0}=\mathbf {H} +\mathbf {M} } ja seuraava suhde sidottuun virtaan: J b o u n d = ∇ × M + ∂ P ∂ t , {\displaystyle \mathbf {J} _{\mathrm {bound} }=\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} {{{partiaalinen t}\\ ,} = J M + J P , {\displaystyle =\mathbf {J} _{\mathrm {M} }+\mathbf {J} _{\mathrm {P} }\ ,} jossa J M = ∇ × M , {\displaystyle \mathbf {J} _{\\mathrm {M} }=\nabla \times \mathbf {M} \ ,} kutsutaan magnetointivirran tiheydeksi, ja J P = ∂ P ∂ t , {\displaystyle \mathbf {J} _{\\mathrm {P} }={\frac {\partial \mathbf {P} {{\partial t}}\ ,} {{partial t}\ ,} on polarisaatiovirran tiheys. Kun otetaan yhtälö B: ∇ × B / μ 0 = ∇ × ( H + M ) {\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {\nabla } \times \left(\mathbf {H+M} \right)} \times \left(\mathbf {H+M} \right)} = ∇ × H + J M {\displaystyle =\mathbf {\nabla } \times \mathbf {H} +\mathbf {J_{M}} } = J f + J P + ε 0 ∂ E ∂ t + J M {\displaystyle =\mathbf {J_{f}} +\mathbf {J_{P}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+\mathbf {J_{M}}+\mathbf {J_{M}} } Näin ollen sidotun virran määritelmään viitaten: ∇ × B / μ 0 = J f + J b o u n d + ε 0 ∂ E ∂ t {\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {J_{f}} +\mathbf {J} _{\mathrm {bound} }+\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}} = J + ε 0 ∂ E ∂ t , {\displaystyle =\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}\ ,} {\partial t}\ ,} kuten oli tarkoitus näyttää.

 

Ampèren laki cgs-yksikköinä

cgs-yksiköissä yhtälön integraalimuoto, mukaan lukien Maxwellin korjaus, on seuraava

∮ C B ⋅ d ℓ = 1 c ∬ S ( 4 π J + ∂ E ∂ t ) ⋅ d S {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}={\frac {1}{c}}\iint _{S}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} }

jossa c on valon nopeus.

Yhtälön differentiaalimuoto (jälleen, mukaan lukien Maxwellin korjaus) on seuraava

∇ × B = 1 c ( 4 π J + ∂ E ∂ t ) . {\displaystyle \mathbf {\nabla } \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right). }  

Aiheeseen liittyvät sivut