Pistetuotto

Matematiikassa pistetuotto on operaatio, joka ottaa syötteenä kaksi vektoria ja palauttaa tuloksena skalaariluvun. Palautettu luku riippuu molempien vektoreiden pituudesta ja niiden välisestä kulmasta. Vaihtoehtoinen nimi skalaarituote korostaa tuloksen skalaarista (eikä vektorista) luonnetta.

Pistetuotto eroaa (kolmiulotteisessa avaruudessa) ristitulosta, jonka tuloksena saadaan vektori.

Määritelmä

Kahden vektorin a = [a₁ , a₂ , ..., a_n ] ja b = [b₁ , b₂ , ..., b_n ] pistetuotto määritellään seuraavasti:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

jossa Σ tarkoittaa summausmerkintää ( kaikkien termien summa) ja n on vektoriavaruuden ulottuvuus.

Mitassa 2 vektoreiden [a,b] ja [c,d] pistetuotto on ac + bd. Samoin ulottuvuudessa 3 vektoreiden [a,b,c] ja [d,e,f] pistetuotto on ad + be + cf. Esimerkiksi kahden kolmiulotteisen vektorin [1, 3, -5] ja [4, -2, -1] pistetuotto on seuraava

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Geometrinen tulkinta

Euklidisessa geometriassa pisteen tulo, pituus ja kulma liittyvät toisiinsa. Vektorille a pistetuotto a - a on a:n pituuden neliö tai

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

missä ||a|| tarkoittaa a:n pituutta (suuruutta). Yleisemmin, jos b on toinen vektori

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

jossa ||a|| ja ||b|| tarkoittavat a:n ja b:n pituuksia ja θ on niiden välinen kulma.

Tämä kaava voidaan järjestää uudelleen kahden nollasta poikkeavan vektorin välisen kulman suuruuden määrittämiseksi:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {\mathbf {a}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)} $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Vektorit voidaan myös ensin muuntaa yksikkövektoreiksi jakamalla ne niiden suuruudella:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

jolloin kulma θ saadaan seuraavasti

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}\cdot {\boldsymbol {\hat {b}})}) $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Koska 90°:n kosini on nolla, kahden kohtisuoran (kohtisuoran) vektorin pistetuotto on aina nolla. Lisäksi kahta vektoria voidaan pitää ortogonaalisena, jos ja vain jos niiden pistetuotto on nolla ja jos molempien pituus on nollasta poikkeava. Tämä ominaisuus tarjoaa yksinkertaisen menetelmän ortogonaalisuusehdon testaamiseen.

Joskus näitä ominaisuuksia käytetään myös pistetuoton määrittelyyn, erityisesti 2- ja 3-ulotteisissa tapauksissa; tämä määritelmä vastaa edellä mainittua. Suuremmissa ulottuvuuksissa kaavaa voidaan käyttää kulman käsitteen määrittelyyn.

Geometriset ominaisuudet perustuvat siihen, että perusta on ortonormaali eli koostuu pareittain kohtisuorista vektoreista, joiden pituus on yksikkö.

Skalaariprojektio

Jos sekä a:n että b:n pituus on yksi (eli ne ovat yksikkövektoreita), niiden pistetulos on yksinkertaisesti niiden välisen kulman kosini.

Jos vain b on yksikkövektori, pistetuotto a - b antaa |a| cos(θ), eli a:n projektion suuruuden b:n suuntaan, ja miinusmerkin, jos suunta on vastakkainen. Tätä kutsutaan a:n skalaariprojektioksi b:hen tai a:n skalaarikomponentiksi b:n suuntaan (ks. kuva). Tällä pistetuoton ominaisuudella on useita hyödyllisiä sovelluksia (ks. esim. seuraava luku).

Jos a tai b ei ole yksikkövektori, niin esimerkiksi a:n projektio b:n suuntaan on suuruudeltaan a - (b / |b|), koska yksikkövektori b:n suuntaan on b / |b|.

Kierto

Ortonormaalin perustan, jonka avulla vektori a esitetään, kierto saadaan kertomalla a kiertomatriisilla R. Tämä matriisikertolasku on vain pistetuotosten sarjan kompakti esitys.

Olkoon esimerkiksi

B₁ = {x, y, z} ja B₂ = {u, v, w} ovat saman avaruuden R³ kaksi erilaista ortonormaalia emäksistä, ja B₂ saadaan kiertämällä vain B₁ ,
a₁ = (a_x , a_y , a_z ) edustaa vektoria a suhteessa B ,₁
a₂ = (a_u , a_v , a_w ) edustavat samaa vektoria pyöritetyn perustan B₂ suhteen,
u₁ , v₁ , w₁ ovat pyöritetyt perusvektorit u, v, w, jotka on esitetty B₁ muodossa.

Tämän jälkeen kierto B₁ :sta B₂ :een suoritetaan seuraavasti:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\{\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Huomaa, että rotaatiomatriisi R muodostetaan käyttämällä sen riveinä rotaatioperusvektoreita u₁ , v₁ , w₁ , ja nämä vektorit ovat yksikkövektoreita. Määritelmän mukaan Ra₁ koostuu sarjasta pistetuotteita R:n kunkin kolmen rivin ja vektorin a₁ välillä. Jokainen näistä pistetuotteista määrittää a:n skalaarikomponentin pyöritetyn perusvektorin suuntaan (ks. edellinen jakso).

Jos₁ on rivivektori eikä sarakevektori, R:n on sisällettävä sarakkeissaan pyöritetyt perusvektorit, ja sen on jälkikerrottava₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}}_{2}={\mathbf {a}}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

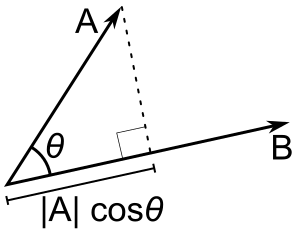
A - B = |A| |B| cos(θ). |A| cos(θ) on A:n skalaariprojektio B:hen.

Fysiikka

Fysiikassa magnitudi on skalaari fysikaalisessa mielessä eli koordinaatistosta riippumaton fysikaalinen suure, joka ilmaistaan numeerisen arvon ja fysikaalisen yksikön tulona, ei pelkkänä lukuna. Myös pistetuotto on tässä mielessä skalaari, joka annetaan kaavalla ja joka on riippumaton koordinaatistosta. Esimerkki:

Mekaaninen työ on voima- ja siirtymävektoreiden pistetuotto.
Magneettivuo on magneettikentän ja pinta-alavektoreiden pistetuotto.
Tilavuusvirta on nesteen nopeuden ja pinta-alavektoreiden pistetuotto.

Ominaisuudet

Seuraavat ominaisuudet pätevät, jos a, b ja c ovat reaalivektoreita ja r on skalaari.

Pistetuotto on kommutatiivinen:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Pistetuotto on distributiivinen vektorien yhteenlaskuun nähden:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Pistetuotos on bilineaarinen:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

Kun kerrotaan skalaarilla, pistetuotto täyttää:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} } $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(nämä kaksi viimeistä ominaisuutta seuraavat kahdesta ensimmäisestä).

Kaksi nollasta poikkeavaa vektoria a ja b ovat kohtisuorassa, jos ja vain jos a - b = 0.

Toisin kuin tavallisten lukujen kertolasku, jossa jos ab = ac, b on aina yhtä suuri kuin c, ellei a ole nolla, pistetuotto ei noudata kumoamislakia:

Jos a - b = a - c ja a ≠ 0, voimme kirjoittaa: a - (b - c) = 0 distributiivilain mukaan; yllä olevan tuloksen mukaan tämä tarkoittaa vain sitä, että a on kohtisuorassa (b - c):tä vastaan, jolloin (b - c) ≠ 0, ja siten b ≠ c.

Jos perusta on ortonormaali, pistetuotto on muuttumaton perustan isometrisissä muutoksissa: rotaatioissa, heijastuksissa ja yhdistelmissä, kun origo pidetään kiinteänä. Edellä mainittu geometrinen tulkinta perustuu tähän ominaisuuteen. Toisin sanoen ortonormaalissa avaruudessa, jossa on mikä tahansa määrä ulottuvuuksia, pistetuotto on muuttumaton ortogonaaliseen matriisiin perustuvassa koordinaattimuunnoksessa. Tämä vastaa seuraavia kahta ehtoa:

Uusi perusta on jälleen ortonormaali (eli se on ortonormaali vanhassa perusta-arvossa ilmaistuna).
Uusilla perusvektoreilla on sama pituus kuin vanhoilla vektoreilla (eli yksikköpituus vanhan perustan suhteen).

Jos a ja b ovat funktioita, a - b:n derivaatta on a' - b + a - b'.

Kolminkertaisen tuotteen laajennus

Tämä on erittäin hyödyllinen identiteetti (tunnetaan myös nimellä Lagrangen kaava), joka sisältää piste- ja ristitulon. Se kirjoitetaan seuraavasti

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )- -\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} } $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

joka on helpompi muistaa muodossa "BAC miinus CAB", kun pidetään mielessä, mitkä vektorit ovat pistemäisiä. Tätä kaavaa käytetään yleisesti vektorilaskelmien yksinkertaistamiseen fysiikassa.

Geometrisen tulkinnan todiste

Tarkastellaan elementtiä R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Pythagoraan lauseen toistuva soveltaminen antaa sen pituudelle |v| seuraavan tuloksen.

| v | 2 = v 1 2 + v 2 2 + . . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Mutta tämä on sama kuin

v ⋅ v = v 1 2 + v 2 2 + . . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

joten voimme päätellä, että vektorin v ja itsensä välinen pistetuotto antaa vektorin pituuden neliön.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Tarkastellaan nyt kahta origosta lähtevää vektoria a ja b, jotka on erotettu toisistaan kulmalla θ. Kolmas vektori c voidaan määritellä seuraavasti

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} {=}}\ \mathbf {a} -\mathbf {b} .\,} \,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

jolloin muodostuu kolmio, jonka sivut ovat a, b ja c. Kosinusten lain mukaan on siis

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} |||\mathbf {b} | \cos \theta .\,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Korvaamalla neliölliset pituudet pistetuotteilla Lemman 1 mukaisesti saadaan seuraava tulos

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Mutta koska c ≡ a - b, meillä on myös seuraavat arvot

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} , $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$

joka jakaantumislain mukaan laajenee muotoon

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Yhdistämällä kaksi c - c -yhtälöä, (1) ja (2), saadaan seuraavat tulokset

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Kun molemmista puolista vähennetään a - a + b - b ja jaetaan -2:lla, saadaan tulokseksi

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

Yleistäminen

Sisätuote yleistää pistetuoton abstrakteille vektoriavaruuksille ja sitä merkitään yleensä seuraavasti: ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . Pistepotentiaalin geometrisen tulkinnan vuoksi vektorin a normi ||a|| tällaisessa sisäisen tuotteen avaruudessa määritellään seuraavasti

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

siten, että se yleistää pituuden, ja kahden vektorin a ja b välinen kulma θ on muotoa

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos \theta }= \frac \langle \mathbf {a} \,,\mathbf {b} \\monikulmio }{\|\mathbf {a} \|\,\|\\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

Erityisesti kaksi vektoria pidetään ortogonaalisina, jos niiden sisäinen tuote on nolla.

⟨ a , b ⟩ = 0. \displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

Jos vektoreissa on kompleksisia merkintöjä, pistetuoton määritelmän käyttäminen johtaisi aivan erilaisiin geometrisiin ominaisuuksiin. Esimerkiksi vektorin ja itsensä välinen pistetuotto voi olla mielivaltainen kompleksiluku, ja se voi olla nolla ilman, että vektori on nollavektori; tällä puolestaan olisi vakavia seurauksia esimerkiksi pituuden ja kulman käsitteille. Monet geometriset ominaisuudet voidaan pelastaa skalaarituoton symmetrisistä ja bilineaarisista ominaisuuksista luopumisen kustannuksella määrittelemällä vaihtoehtoisesti

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

missä b_i on b _ikompleksikonjugaatti. Tällöin minkä tahansa vektorin skalaaritulo itsensä kanssa on ei-negatiivinen reaaliluku, ja se on nollasta poikkeava lukuun ottamatta nollavektoria. Tämä skalaarituote ei kuitenkaan ole lineaarinen b:n suhteen (vaan pikemminkin konjugatiivinen lineaarinen), eikä skalaarituote ole myöskään symmetrinen, koska

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Tämäntyyppinen skalaarituote on kuitenkin varsin hyödyllinen, ja se johtaa Hermitin muodon ja yleisten sisäisten tuoteavaruuksien käsitteisiin.

Frobeniuksen sisäinen tuote yleistää pistetuoton matriiseihin. Se määritellään kahden samankokoisen matriisin vastaavien komponenttien tuotteiden summana.

Yleistäminen tensoreihin

Järjestysasteeltaan n:n tensorin ja järjestysasteeltaan m:n tensorin välinen pistetuotto on järjestysasteeltaan n+m-2. Pistetuotto saadaan kertomalla ja summaamalla molempien tensoreiden yksi indeksi. Jos A {\displaystyle \mathbf {A} } $\mathbf {A}$ ja B {\displaystyle \mathbf {B} } $\mathbf {B}$ ovat kaksi tensoria, joiden alkioesitys A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} $A_{ij\dots }^{k\ell \dots }$ ja B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}}} $B_{mn\dots }^{p{\dots }i}$ on pistepotentiaalin A ⋅ B {\displaystyle \mathbf {A}} elementit. \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ ovat seuraavat

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Tämä määritelmä redusoituu luonnollisesti tavalliseen vektorien pistetuotteeseen, kun sitä sovelletaan vektoreihin, ja matriisien kertolaskuun, kun sitä sovelletaan matriiseihin.

Toisinaan kaksinkertaista pistetuotosta käytetään kuvaamaan kahden indeksin kertomista ja yhteenlaskua. Kahden 2. kertaluvun tensorin välinen kaksinkertainen pistetuotto on skalaari.

Aiheeseen liittyvät sivut

Cauchy-Schwarzin epätasa-arvo
Ristikkäinen tuote
Matriisien kertominen
Fysiikka

Kysymyksiä ja vastauksia

K: Mikä on pistetuotto matematiikassa?

V: Pistetuotto on operaatio, joka ottaa syötteenä kaksi vektoria ja palauttaa tuloksena skalaariluvun.

K: Mistä pistetuotto riippuu?

V: Pistetuotto riippuu molempien vektoreiden pituudesta ja niiden välisestä kulmasta.

K: Miksi pistetuoton nimi on johdettu keskitetystä pisteestä "-"?

V: Nimi on johdettu keskitetystä pisteestä "-", jota käytetään usein tämän operaation nimeämiseen.

K: Mikä on pistetulon vaihtoehtoinen nimi?

V: Vaihtoehtoinen nimi on skalaarituote, joka korostaa tuloksen skalaarista (eikä vektorista) luonnetta.

K: Mikä on pistetuoton ja ristitulon välinen ero kolmiulotteisessa avaruudessa?

V: Pistetuotto tuottaa tulokseksi skalaariluvun, kun taas ristituotto tuottaa tulokseksi vektorin.

K: Mihin pistetuotosta käytetään matematiikassa?

V: Pistepotentiaalin avulla voidaan määrittää, ovatko kaksi vektoria kohtisuorassa (90 asteen kulmassa), ja projisoida yksi vektori toisen vektorin päälle.

K: Voidaanko pistetuotosta käyttää korkeampiulotteisissa tiloissa?

V: Kyllä, pistetuotto voidaan laajentaa korkeampiulotteisiin tiloihin yleistämällä määritelmä.