Valonnopeus
Valon nopeus tyhjässä avaruudessa on universaali fysikaalinen vakio. Se tarkoittaa, että se on sama kaikkialla tyhjässä avaruudessa eikä muutu ajan myötä. Fyysikot käyttävät usein kirjainta c merkitsemään valon nopeutta tyhjässä tilassa (tyhjiössä). Se on määritelmän mukaan täsmälleen 299 792 458 metriä sekunnissa (983 571 056 jalkaa sekunnissa). Fotoni (valohiukkanen) kulkee tällä nopeudella tyhjiössä.
Erityisen suhteellisuusteorian mukaan c on maksiminopeus, jolla kaikki energia, aine ja fyysinen informaatio maailmankaikkeudessa voivat liikkua. Se on kaikkien massattomien hiukkasten, kuten fotonien, ja niihin liittyvien kenttien - myös sähkömagneettisen säteilyn, kuten valon - nopeus tyhjiössä.
Nykyinen teoria ennustaa sen olevan painovoiman nopeus (eli gravitaatioaallot). Tällaiset hiukkaset ja aallot kulkevat c:n nopeudella riippumatta lähteen liikkeestä tai havaitsijan inertiaaliviitekehyksestä. Suhteellisuusteoriassa c yhdistää avaruuden ja ajan, ja se esiintyy kuuluisassa massa-energia-ekvivalenssin yhtälössä E = mc2.
Erityinen suhteellisuusteoria perustuu havaintojen toistaiseksi vahvistamaan ennusteeseen, jonka mukaan valon mitattu nopeus tyhjiössä on sama riippumatta siitä, liikkuvatko valon lähde ja mittauksen suorittaja toisiinsa nähden vai eivät. Tämä ilmaistaan joskus sanoilla "valon nopeus on riippumaton viitekehyksestä".
Esimerkki
Tämä käyttäytyminen poikkeaa tavanomaisista käsityksistämme liikkeestä, kuten tämä esimerkki osoittaa:
George seisoo maassa junaradan vieressä. Juna kiitää ohi 48 km/h (30 mph) nopeudella. Yrjö heittää pesäpalloa 140 km/h (90 mph) nopeudella junan kulkusuuntaan. Tomilla, junan matkustajalla, on laite (kuten tutkapyssy), jolla mitataan heittonopeuksia. Koska hän on junassa, Tom liikkuu jo 48 km/h (30 mph) heittosuuntaan, joten Tom mittaa pallon nopeudeksi vain 97 km/h (60 mph).
Toisin sanoen Tomin junassa mittaama pesäpallon nopeus riippuu junan nopeudesta.
Yllä olevassa esimerkissä juna liikkui 1/3 pallon nopeudesta, ja junasta mitattu pallon nopeus oli 2/3 maasta mitatusta heittonopeudesta.
Toista nyt koe valolla pesäpallon sijasta, eli Yrjöllä on taskulamppu sen sijaan, että hän heittäisi pesäpalloa. Yrjöllä ja Tomilla on molemmilla samanlaiset laitteet valon nopeuden mittaamiseen (baseball-esimerkin tutkapyssyn sijaan).
George seisoo maassa junaradan vieressä. Juna kiitää ohi 1/3 valonnopeudella. Yrjö väläyttää valonsäteen junan kulkusuuntaan. George mittaa valon nopeudeksi 186 282 mailia sekunnissa (299 792 kilometriä sekunnissa). Tom, junan matkustaja, mittaa valonsäteen nopeuden. Minkä nopeuden Tom mittaa?
Intuitiivisesti voisi ajatella, että taskulampusta tulevan valon nopeuden pitäisi olla junassa mitattuna 2/3 maasta mitatusta nopeudesta, aivan kuten pesäpallon nopeus oli 2/3. Itse asiassa junasta mitattu nopeus on kuitenkin täysi arvo, 186 282 mailia sekunnissa (299 792 kilometriä sekunnissa), eikä 124 188 mailia sekunnissa (199 861 kilometriä sekunnissa).
Se kuulostaa mahdottomalta, mutta sitä mitataan. Osasyynä on se, että valo on energiaa, joka toimii ja liikkuu hyvin eri tavoin kuin aine tai kiinteät esineet, kuten pesäpallo.
Maxwellin yhtälöt ennustivat valon nopeuden ja vahvistivat Michael Faradayn ajatuksen siitä, että valo on sähkömagneettinen aalto (energian liikkumistapa). Näistä yhtälöistä käy ilmi, että valon nopeus on yhteydessä vapaan tilan permittiivisyyden ε0 ja vapaan tilan permeabiliteetin μ0 neliöjuuren käänteislukuun:
c = 1 ε 0 μ 0 . {\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ . } 
Tästä seuraa, että mikään ei voi kulkea valonnopeutta nopeammin. Toinen seuraus on se, että riippumatta siitä, kuinka paljon energiaa käytetään kohteen nopeuden kasvattamiseen, se tulee yhä lähemmäksi ja lähemmäksi, mutta ei koskaan saavuta valonnopeutta. Nämä ajatukset löysi 1900-luvun alussa Albert Einstein, jonka työ muutti täysin käsityksemme valosta.
Kirkkaan materiaalin taitekerroin on tyhjiössä olevan valon nopeuden ja kyseisessä materiaalissa olevan valon nopeuden suhde.
Mittaus
Rømer
Ole Christensen Rømer käytti tähtitieteellistä mittausta tehdäkseen ensimmäisen kvantitatiivisen arvion valon nopeudesta. Maasta mitattuna kaukana olevaa planeettaa kiertävien kuiden kiertoaika on lyhyempi, kun Maa lähestyy planeettaa, kuin kun Maa etääntyy siitä. Etäisyys, jonka valo kulkee planeetalta (tai sen kuulta) Maahan, on lyhyempi, kun Maa on kiertoradallaan pisteessä, joka on lähimpänä planeettaa, kuin kun Maa on kiertoratansa kaukaisimmassa pisteessä, ja etäisyysero on Maan auringon kiertoradan halkaisija. Havaittu muutos kuun kiertoaikajaksossa on itse asiassa ero ajassa, joka valolla kuluu lyhyemmän tai pidemmän matkan kulkemiseen. Rømer havaitsi tämän ilmiön Jupiterin sisimmän kuun Ion kohdalla ja päätteli, että valolla kestää 22 minuuttia ylittää Maan kiertoradan halkaisija.
Bradley
Toinen menetelmä on käyttää valon aberraatiota, jonka James Bradley löysi ja selitti 1700-luvulla. Tämä ilmiö syntyy kaukaisesta lähteestä (kuten tähdestä) tulevan valon nopeuden ja sen havaitsijan nopeuden vektorin summautumisesta (ks. kaavio oikealla). Liikkuva havaitsija näkee siis valon tulevan hieman eri suunnasta ja näkee näin ollen lähteen alkuperäisestä sijainnistaan siirtyneenä. Koska Maan nopeuden suunta muuttuu jatkuvasti Maan kiertäessä Aurinkoa, tämä vaikutus aiheuttaa tähtien näennäisen sijainnin siirtymisen. Tähtien sijainnin kulmaeron perusteella voidaan ilmaista valon nopeus maapallon nopeutena auringon ympäri. Kun tiedetään vuoden pituus, tämä voidaan helposti muuntaa ajaksi, joka kuluu Auringosta Maahan. Vuonna 1729 Bradley käytti tätä menetelmää päätelläkseen, että valo kulkee 10 210 kertaa nopeammin kuin Maa kiertoradallaan (nykyään se kulkee 10 066 kertaa nopeammin) tai että valolta kestää 8 minuuttia 12 sekuntia kulkea Auringosta Maahan.
Moderni
Nykyään "valoaika etäisyysyksikköä kohti" - c:n käänteisluku (1/c), joka ilmaistaan sekunteina astronomista yksikköä kohti - mitataan vertailemalla aikaa, jonka radiosignaalit ehtivät eri avaruusaluksiin Aurinkokunnassa. Avaruusalusten sijainti lasketaan Auringon ja eri planeettojen gravitaatiovaikutusten perusteella. Yhdistämällä monia tällaisia mittauksia saadaan paras sopiva arvo valon kuluttamalle ajalle etäisyysyksikköä kohti. Kansainvälisen tähtitieteellisen liiton (IAU) hyväksymä paras arvio vuonna 2009[päivitys] on:
valoaika etäisyysyksikköä kohti: 499.004783836(10) s
c = 0,00200398880410(4) AU/s.
c = 173,144632674(3) AU/vrk.
Näiden mittausten suhteellinen epävarmuus on 0,02 osaa miljardissa (2×10-11), mikä vastaa interferometristen pituusmittausten epävarmuutta Maassa. Koska metri määritellään valon tietyssä aikaväliajassa kulkemaksi pituudeksi, valon ajan mittaaminen etäisyysyksikköä kohti voidaan tulkita myös AU:n pituuden mittaamiseksi metreinä. Metriä pidetään varsinaisen pituuden yksikkönä, kun taas AU:ta käytetään usein tietyssä viitekehyksessä havaitun pituuden yksikkönä.
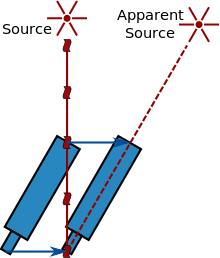
Valon aberraatio: Kaukaisesta lähteestä tuleva valo näyttää liikkuvan teleskoopin silmissä tulevan eri paikasta, koska valon nopeus on rajallinen.
Käytännön vaikutukset
Valon rajallinen nopeus on merkittävä este pitkien matkojen avaruusmatkoille. Jos oletetaan matka Linnunradan toiselle puolelle, viestin ja siihen vastaamisen kokonaisaika olisi noin 200 000 vuotta. Vielä vakavampaa on se, että mikään avaruusalus ei pystyisi kulkemaan valoa nopeammin, joten kaikki galaktisen mittakaavan kuljetukset olisivat käytännössä yksisuuntaisia, ja ne kestäisivät paljon kauemmin kuin mikään nykyaikainen sivilisaatio on ollut olemassa.
Valon nopeus voi myös olla ongelma hyvin lyhyillä etäisyyksillä. Supertietokoneissa valon nopeus asettaa rajoituksen sille, kuinka nopeasti tietoja voidaan lähettää prosessorien välillä. Jos prosessori toimii yhden gigahertsin nopeudella, signaali voi kulkea enintään noin 30 senttimetriä yhdessä syklissä. Siksi prosessorit on sijoitettava lähelle toisiaan, jotta tiedonsiirtoviiveet olisivat mahdollisimman pienet; tämä voi aiheuttaa ongelmia jäähdytyksen kanssa. Jos kellotaajuudet kasvavat edelleen, valon nopeudesta tulee lopulta rajoittava tekijä yksittäisten sirujen sisäisessä suunnittelussa.
Kysymyksiä ja vastauksia
K: Mikä on valon nopeus?
V: Valon nopeus, jota merkitään kirjaimella "c", on fysikaalinen vakio, joka on täsmälleen 299 792 458 metriä sekunnissa (983 571 056 jalkaa sekunnissa).
K: Miten valon nopeus esitetään?
V: Valon nopeus merkitään yleensä c:llä, ja tyhjiössä se merkitään erityisesti c^0:lla.
K: Mitkä hiukkaset kulkevat valon nopeudella?
V: Fotonit (valohiukkaset) liikkuvat tällä nopeudella tyhjiössä. Lisäksi kaikki massattomat hiukkaset, kuten fotonit ja niihin liittyvät kentät - myös sähkömagneettinen säteily, kuten valo - kulkevat c:n nopeudella riippumatta niiden lähteestä tai tarkkailijan inertiaaliviitekehyksestä.
K: Mitä erityinen suhteellisuusteoria sanoo valon nopeudesta?
V: Erityisen suhteellisuusteorian mukaan c on suurin nopeus, jolla kaikki energia, aine ja fysikaalinen informaatio voivat liikkua maailmankaikkeudessa. Sen mukaan valon mitattu nopeus tyhjiössä pysyy muuttumattomana riippumatta siitä, liikkuvatko valon lähde tai havaitsija toisiinsa nähden.
K: Miten c liittyy avaruuteen ja aikaan?
V: Suhteellisuusteoriassa c yhdistää avaruuden ja ajan, koska se esiintyy Einsteinin kuuluisassa yhtälössä E = mc2. Tämä yhtälö osoittaa, miten energia voidaan muuttaa massaksi ja päinvastoin.
K: Onko olemassa todisteita, jotka tukevat erityissuhteellisuusteorian ennustusta mitatusta valon nopeudesta?
V: Kyllä - tähän mennessä tehdyt havainnot ovat tukeneet ennustusta, jonka mukaan mitattu nopeus pysyy vakiona riippumatta siitä, mistä viitekehyksestä valoa tarkkaillaan tai mitä sen lähde kulkee.
