Heisenbergin epätarkkuusperiaate | myös Heisenbergin epävarmuusperiaate

Kaaviot

 
6. Tässä animaatiossa näkyy yksi maailmankaikkeuden epävarmuuden tärkeistä seurauksista: elektronien kvanttitunnelointi. Katso tarkkaan. Joka kerta pieni pala pääsee esteen läpi.  


5. Keskimmäisen aukon ripustaminen jousivaakojen avulla mahdollistaa momentin mittaamisen, mutta se liikuttaa aukkoa arvaamattomasti, joten tieto kunkin fotonin sijainnista keskellä katoaa.  


4. Jousi, joka kiinnitetään esteeseen, jossa on pieni reikä, saa hiukkasen puristumaan reiän läpi, mikä työntää estettä, venyttää jousia ja mittaa näin vauhtia. Mutta koska jousitettu este liikkuu, emme ole yhtä varmoja siitä, missä hiukkanen oli, kun se meni reiän läpi, ja diffraktio vaikuttaa myös hiukkasen sijaintiin havaintoruudulla.  


1. Fotonit, elektronit ja muut subatomiset hiukkaset tarkentuvat terävästi, kun ne ammutaan suuren reiän läpi, mutta emme tiedä tarkalleen, missä ne olivat matkan puolivälissä.  


2. Reiän kaventaminen taivuttaa hiukkasten reittejä reiän reunoilla (diffraktio), joten syntyvä säde kasvaa ja pehmenee.  


3. Reiän kaventaminen lisää varmuutta siitä, missä fotoni on keskellä, mutta sen suunta sieltä oikealla olevaan havaintoruutuun muuttuu vastaavasti epävarmemmaksi. Tarkennus hämärtyy. Reiän laajentaminen saa kaikki fotonit päätymään havaintoruudun keskelle, mutta tällöin meillä on huonompi käsitys siitä, missä ne olivat, kun ne menivät keskimmäisen esteen läpi.  

Miten ihmiset oppivat epävarmuudesta?

Hyvin pian sen jälkeen, kun Werner Heisenberg oli luonut uuden kvanttifysiikan, hänen matematiikastaan nousi esiin jotain odottamatonta, nimittäin ilmaisu:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }\qquad \qquad \qquad \qquad }

Sijainnin (x) virheen vaihteluväli kertaa impulssin (p) virheen vaihteluväli on suunnilleen yhtä suuri tai suurempi kuin Planckin vakio jaettuna 4π:llä.

Näillä symboleilla muunnetaan matemaattiseen muotoon se, mitä olet jo nähnyt yllä olevissa kuvissa. Symbolit kertovat selkeästi, että et voi olla täysin varma siitä, missä jokin on ja mihin se on menossa. Jos saat selkeämmän käsityksen siitä, missä se on milloinkin, sinulla on vähemmän käsitystä siitä, missä se on menossa ja kuinka nopeasti. Jos saatte selvemmän käsityksen siitä, mihin se on menossa ja kuinka nopeasti milloin tahansa, teillä on vähemmän käsitystä siitä, missä se on juuri nyt.

Tutkijat olivat jo oppineet, miksi tietyt aineet antavat valolle ominaisia värejä, kun niitä kuumennetaan tai muutoin stimuloidaan. Heisenberg yritti selittää, miksi näillä väreillä on kullekin ominainen kirkkaus. Ei olisi riittänyt, jos hän ja muut tiedemiehet olisivat vain sanoneet: "No, näin se vain on". He olivat varmoja siitä, että näille eroille oli oltava hyvä syy ja sille, että kirkkaiden viivojen voimakkuuksien väliset suhteet olivat aina samat kussakin alkuaineen näytteessä.

Hänellä ei ollut aavistustakaan siitä, että hän törmäisi luonnon kätkettyyn salaisuuteen, kun hän lähti etsimään selitystä kullekin alkuaineelle ominaisten värillisten viivojen voimakkuudelle. Kvanttimekaniikan tutkimus oli jo osoittanut, miksi vedyllä on neljä kirkasta viivaa siinä spektrin osassa, jonka ihminen voi nähdä. Näytti varmaan siltä, että seuraavaksi olisi vain opittava, miten niiden kirkkaus voitaisiin laskea. Vety näytti olevan ilmeinen paikka aloittaa, koska vedyllä on vain yksi elektroni ja vain neljä viivaa spektrin näkyvässä osassa. Varmasti täytyy olla hyvä syy siihen, että ne eivät ole yhtä kirkkaita. Selitys neonin ja muiden alkuaineiden eriväristen viivojen kirkkauteen saattoi odottaa.

Heisenberg aloitti kvanttifysiikan tutkimisen mukauttamalla klassisia sähkön yhtälöitä, jotka ovat alun perin hyvin monimutkaisia, joten hänen vuonna 1925 julkaistun artikkelinsa taustalla olevaa matematiikkaa oli hyvin vaikea seurata.

Hän yritti löytää oikean tavan laskea kirkkaiden viivojen voimakkuutta vetylamppujen spektrissä. Hänen oli löydettävä siihen liittyvä suure nimeltä "amplitudi" ja kerrottava amplitudi amplitudilla (tai toisin sanoen hänen oli neliöitävä amplitudi) saadakseen haluamansa intensiteetin. Hänen oli keksittävä, miten amplitudi ilmaistaan tavalla, jossa otetaan huomioon se, että vetylamput eivät säteile kaikilla taajuuksilla eivätkä säteile jatkuvalla taajuusalueella siinä spektrin osassa, jonka ihmiset voivat nähdä. Heisenberg löysi huomattavan uuden tavan laskea amplitudi.

Outo yhtälö, jonka Heisenberg löysi ja jota hän käytti yhden kvanttisuureen (esim. sijainnin) kertomiseen toisella (esim. impulssilla), julkaistiin heinäkuussa 1925 ilmestyneessä "Heisenbergin 'maagisessa' paperissa".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Yllä oleva matematiikka näyttää hyvin vaikealta, mutta sitä edeltävä matematiikka on paljon vaikeampaa ja sitä on erittäin vaikea ymmärtää. Se on esitetty tässä vain siksi, että näyttäisi siltä, miltä se näytti. Heisenbergin artikkeli on historiallinen merkkipaalu. Monet fysiikantutkijat, jotka lukivat hänen paperinsa, sanoivat, että he eivät voineet olla eri mieltä hänen johtopäätöstensä kanssa, mutta että he eivät voineet seurata hänen selitystään siitä, miten hän päätyi näihin johtopäätöksiin. Heisenbergin käyttämät alkuyhtälöt sisälsivät Fourier-sarjoja, ja niihin sisältyi monia tekijöitä. Palaamme yllä olevaan yhtälöön, koska se on eräänlainen resepti matriisien kirjoittamiseen ja kertomiseen.

Uusien yhtälöiden täytyi olla niin outoja ja epätavallisia, koska Heisenberg kuvasi outoa maailmaa, jossa jotkin asiat, kuten elektronien radat, eivät hitaasti suurene tai pienene. Uudenlaisiin muutoksiin liittyy hyppyjä ja suuria välejä hyppyjen välillä. Elektronit voivat hypätä vain tiettyjen ratojen välillä, ja ratojen välillä tapahtuvassa vaihtelussa saavutettu tai menetetty energia syntyy, kun oikean energian omaava fotoni absorboituu tai uusi oikean energian omaava fotoni syntyy. Jos vetyatomien elektronit hyppäävät (putoavat) useimmiten kahden tietyn radan välillä, kyseisellä energiatasolla emittoituu enemmän fotoneja, joten kyseisellä tasolla tuotettu valo on voimakkainta.

Oli vaikeaa saada jatkuville spektreille (joita näet, kun auringon valo kulkee prisman läpi) rakennettuja yhtälöitä sovitettua spektreihin, joissa on vain muutama huipputaajuus, joiden välillä ei ole mitään. Lähes kaikki, mitä valosta ja energiasta oli jo opittu, oli tehty suurilla esineillä, kuten palavilla kynttilöillä tai auringolla, ja nämä suuret esineet tuottavat kaikki jatkuvia spektrejä. Vaikka näillä tavallisen kokoisilla esineillä oli helppo tehdä kokeita, oli silti kestänyt kauan selvittää niitä sääteleviä (fysiikan)lakeja. Nyt fyysikot olivat tekemisissä liian pienten esineiden kanssa, jotka eivät tuottaneet jatkuvia spektrejä, ja he yrittivät löytää keinon, jolla he saisivat ainakin vihjeitä siitä, mitä he jo tiesivät, ja joka auttaisi heitä löytämään näiden pienten ja hajanaisten valonlähteiden lait.

Alkuperäisissä yhtälöissä käsiteltiin eräänlaista värähtelevää kehoa, joka tuottaisi aallon, vähän samaan tapaan kuin kieli uruissa tuottaisi ääniaallon, jolla on ominaistaajuus. Eli oli liikettä edestakaisin (kuten kielikielellä) ja syntyi emittoitunut aalto, joka voitiin esittää siniaaltona. Suuri osa siitä, mitä aiemmin oli selvitetty fysiikasta atomitasolla, liittyi elektronien liikkumiseen ytimien ympärillä. Kun massa liikkuu kiertoradalla, kun se pyörii jonkin keskipisteen ympärillä, sillä on niin sanottu "kiertomomentti". Kulmavauhti on tapa, jolla jokin karusellin kaltainen laite jatkaa pyörimistä sen jälkeen, kun ihmiset ovat lopettaneet sen työntämisen. Vaihelaskelmissa ja kulmamomentissa käytetty matematiikka on monimutkaista. Kaiken lisäksi Heisenberg ei esittänyt kaikkia laskutoimituksiaan vuonna 1925 julkaistussa artikkelissaan, joten hyvilläkin matemaatikoilla voi olla vaikeuksia selvittää, mitä hän ei sanonut.

Vaikka monet fyysikot sanoivat, etteivät he kyenneet ymmärtämään Heisenbergin läpimurtopaperin eri matemaattisia vaiheita, eräässä tuoreessa artikkelissa, jossa yritetään selittää, miten Heisenberg sai tuloksensa, käytetään kaksikymmentä matematiikkaa sisältävää sivua. Edes tätä artikkelia ei ole helppo ymmärtää. Matematiikka alkoi todella vaikeista asioista ja johti lopulta johonkin suhteellisen yksinkertaiseen tulokseen, joka on esitetty tämän artikkelin yläosassa. Yksinkertaisempaan tulokseen pääseminen ei ollut helppoa, emmekä yritä näyttää prosessia, jolla päästään vanhentuneesta kuvasta maailmankaikkeudesta uuteen kvanttifysiikkaan. Tarvitsemme vain tarpeeksi yksityiskohtia osoittaaksemme, että melkein heti Heisenbergin läpimurtonsa jälkeen näkyviin tuli osa maailmankaikkeuden toiminnasta, jota kukaan ei ollut koskaan aiemmin nähnyt.

Heisenbergin on täytynyt olla hyvin innoissaan mutta myös hyvin väsynyt, kun hän myöhään illalla vihdoin teki läpimurtonsa ja alkoi todistaa itselleen, että se toimisi. Melkein heti hän huomasi jotakin outoa, jotakin, jota hän piti ärsyttävänä pienenä ongelmana, jonka hän voisi saada jotenkin poistumaan. Mutta kävi ilmi, että tämä pieni riesa olikin suuri löytö.

Heisenberg oli pyrkinyt kertomaan amplitudit amplitudilla, ja nyt Heisenbergillä oli hyvä tapa ilmaista amplitudi uuden yhtälönsä avulla. Luonnollisesti hän ajatteli kertolaskua ja sitä, miten hän kertoisi asioita, jotka annettiin monimutkaisten yhtälöiden muodossa.

Heisenberg tajusi, että amplitudin neliöimisen lisäksi hän haluaisi lopulta kertoa sijainnin impulssilla tai energian ajalla, ja näytti siltä, että näissä uusissa tapauksissa järjestyksen kääntämisellä olisi merkitystä. Heisenbergin mielestä ei pitänyt olla väliä sillä, kerrotaanko sijainti impulssilla vai kerrotaanko impulssi sijainnilla. Jos ne olisivat olleet pelkkiä lukuja, ongelmaa ei olisi ollut. Molemmat olivat kuitenkin monimutkaisia yhtälöitä, ja se, miten numerot saatiin yhdistettyä yhtälöihin, osoittautui erilaiseksi riippuen siitä, kummasta suunnasta lähdettiin liikkeelle. Luonnossa piti ensin mitata sijainti ja sitten impulssi, tai sitten piti ensin mitata impulssi ja sitten sijainti, ja matematiikassa vallitsi sama yleinen tilanne. (Katso englanninkielisen Wikipedian artikkeli Heisenberg's entryway to matrix mechanics, jos haluat oppia hankalia yksityiskohtia!) Tulosten väliset pienet mutta ärsyttävät erot jäisivät, vaikka Heisenberg kuinka toivoi niiden katoavan.

Tuolloin Heisenberg ei päässyt eroon tuosta yhdestä pienestä ongelmasta, mutta hän oli uupunut, joten hän luovutti työnsä välittömälle esimiehelleen Max Bornille ja lähti lomalle.

Max Born oli merkittävä matemaatikko, joka huomasi pian, että Heisenbergin antama yhtälö oli eräänlainen resepti matriisin kirjoittamiseen. Tohtori Born oli tuohon aikaan yksi harvoista ihmisistä, jotka olivat kiinnostuneita tästä oudosta matematiikasta, jota useimmat ihmiset eivät pitäneet kovinkaan hyvänä. Hän tiesi, että matriiseja voitiin kertoa, joten kaikki laskutoimitukset yhden fysiikan ongelman laskemiseksi voitiin hoitaa kertomalla yksi matriisi toisella. Kun monimutkainen menettely saataisiin vakiomuotoiseen ja hyväksyttävään muotoon, se helpottaisi työskentelyä. Se saattaisi myös helpottaa muiden ihmisten hyväksyntää.

Born oli niin hyvä matemaatikko, että hän tajusi melkein heti, että kahden matriisin kertomisen järjestyksen vaihtaminen tuottaisi erilaisen tuloksen, ja tulokset eroaisivat toisistaan vain vähän. Tämä määrä olisi h/2πi. Jokapäiväisessä elämässä tämä ero olisi niin pieni, ettemme edes huomaisi sitä.

 
Auringon koko visuaalinen spektri. Aukkoja ei ole. Tämä kaavio näyttää intensiteetit eri taajuuksilla.  


Kaksi aaltoa, jotka eivät ole keskenään samassa vaiheessa.  


Neon spektri  


Vedyn spektri  


Kun tietyt molekyylit kiihottuvat, ne saavat aikaan ominaisvärin.  

Epävarmuuden muodolliseen teoriaan

Kesti pari vuotta, mutta Heisenberg pystyi todistamaan epävarmuusperiaatteen, joka sanoo, että Δx × Δp = h/2, joka on luku, joka tulee alkuperäisistä yhtälöistä, mutta jättää pois π:n ja i:n, jotka liittyvät faasimuutoksiin. Heisenberg selitti, että hän johti epävarmuusperiaatteensa tästä aiemmasta tuloksesta kirjoittaessaan vuonna 1927 artikkelin, jossa hän esitteli tämän teorian.

Vakio, jota kutsutaan Planckin vakioksi, on salaperäinen luku, joka esiintyy usein, joten meidän on ymmärrettävä, mikä tämä pieni luku on. Numeerisesti se ilmoitetaan yleensä 6,62607×10^-34 J s (joulusekuntia). Se on siis suure, johon liittyy energiaa ja aikaa.

Se löydettiin, kun Planck tajusi, että täydellisen säteilijän (mustan kappaleen säteilijä) energia säteilee tietyn kokoisina yksikköinä, joita kutsutaan "kvanteiksi" (tämän sanan yksikössä on "kvantti"). Säteilyenergia säteilee fotoneina, ja fotonin taajuus on verrannollinen sen antamaan "iskuun". Koemme näkyvän valon eri taajuudet eri väreinä. Spektrin violetissa päässä kullakin fotonilla on suhteellisen suuri energiamäärä; spektrin punaisessa päässä kullakin fotonilla on suhteellisen pieni energiamäärä. Fotonin energiamäärä voidaan laskea yhtälön E = hν avulla (energia on yhtä kuin Planckin vakio kertaa "nu" eli taajuus).

Heisenbergin epävarmuusperiaate Δx × Δp ≥ h kertoo, että aina kun yritämme määrittää tiettyjä numeropareja, pääsemme vain niin lähelle ja että jos yritämme saada selvyyttä toiseen niistä, eli jos yritämme tehdä Δx:stä pienemmän niin, että saamme paremman käsityksen jonkin asian sijainnista, meidän on saatava takaisin isompi luku parin toiselle numerolle, ja että määrä, jonka nämä kaksi poikkeavat toisistaan, liittyy läheisesti h:hen.

Toinen fysikaalisten suureiden pari noudattaa epävarmuussuhdetta: ΔE × Δt ≥ h, ja tämä pari osoittaa muun muassa sen, että jos katsomme tähtienväliseen avaruuteen, johonkin paikkaan, josta emme odottaisi löytävämme mitään, ja pienennämme Δt:tä yhä lähemmäs ja lähemmäs nollaa, yhtälössä esitetyn tasapainon säilyttämiseksi ΔE:n on kasvettava koko ajan suuremmaksi ja suuremmaksi - ja yhtäkkiä jotain, jolla on vauhtia, voi ilmestyä olemassaoloon vain tuoksi lyhyeksi ajaksi.

Miten tämä määrittelemättömyys (varmuuden puute) on selitettävissä? Mitä maailmankaikkeudessa tapahtuu? Usein sanotaan, että onnistunut uusi teoria voi antaa uutta tietoa tutkittavasta ilmiöstä. Heisenberg loi matemaattisen mallin, joka ennusti oikeat intensiteetit vedyn kirkasviivaspektrille, mutta tarkoituksetta hän havaitsi, että tietyt fysikaalisten suureiden parit paljastavat odottamattoman epävarmuuden. Siihen asti kenelläkään ei ollut aavistustakaan siitä, että mittauksia ei voisi ikuisesti tehdä yhä tarkemmiksi ja täsmällisemmiksi. Se, että niitä ei voitu tehdä entistä varmemmiksi, entistä varmemmiksi, oli hämmästyttävä uusi löytö. Monet ihmiset eivät olleet halukkaita hyväksymään sitä.

Bohr ja hänen kollegansa väittivät, että fotoneilla, elektroneilla jne. ei ole sijaintia eikä impulssia ennen kuin ne mitataan. Tämä teoreettinen kanta syntyi epävarmuuden löytymisen seurauksena, eikä se ollut vain henkilökohtainen mieltymys siitä, mihin uskoa. Bohrin mukaan emme tiedä mitään fotonin tai elektronin kaltaisesta asiasta ennen kuin havaitsemme sen. Jotta voisimme havainnoida näin pientä asiaa, meidän on oltava jotenkin vuorovaikutuksessa sen kanssa. Jokapäiväisessä elämässä on mahdollista esimerkiksi kävellä auton rinnalla ja merkitä ylös, milloin auto ylittää jalkakäytävälle piirretyn ruudukon pisteitä. Ehkäpä itse auton paino painaa jalkakäytävässä olevia pieniä vipuja, jotka käynnistävät niihin kiinnitetyt kellot ja kirjaavat ylös auton painon. Loppujen lopuksi meillä olisi selkeä muistiinpano siitä, missä auto oli eri aikoina, ja voisimme myös laskea sen kulkusuunnan ja painon. Tällöin voisimme tietää milloin tahansa kellon aikana sekä auton sijainnin että sen liikemäärän (nopeus kerrottuna massalla). Emme voisi edes kuvitella, että pienten vipujen liikuttamiseen tarvittava voima vaikuttaisi mitenkään auton kulkuun. Emme myöskään kuvittelisi, että autolla ei olisi sijaintia tai liikerataa niiden jalkakäytävän kohtien välillä, joissa on vipuja, tai että auto on noina aikoina olemassa jonkinlaisessa kolmiulotteisessa sumeassa tilassa ja asettuu paikalleen vain silloin, kun se painaa vipua. Meille tuttu maailma ei paljasta tällaisia outoja vuorovaikutussuhteita.

Jotta voisimme paikantaa laivan merellä pimeimpänä yönä, voisimme käyttää hakuvaloa, eikä valo häiritsisi laivan sijaintia tai kulkusuuntaa, mutta elektronin paikantaminen valon avulla edellyttäisi, että siihen osuisi yksi tai useampi fotoni, joilla kaikilla on tarpeeksi vauhtia häiritäkseen elektronin sijaintia ja lentorataa. Elektronin paikantaminen muilla keinoin edellyttäisi sen pitämistä jonkinlaisessa fyysisessä rajoituksessa, joka myös lopettaisi sen etenemisliikkeen.

Fotonin paikantamiseksi voidaan sen etenemisliikettä keskeyttämättä parhaimmillaan saada se kulkemaan esteessä olevan ympyränmuotoisen reiän läpi. Jos tiedetään aika, jolloin fotoni lähetettiin (esimerkiksi laserilla), ja aika, jolloin fotoni saapuu havaintoruutuun, kuten digitaalikameraan, voidaan laskea aika, joka kului tämän matkan kulkemiseen, ja aika, jolloin fotoni kulki reiän läpi. Jotta fotoni voisi kulkea sen läpi, pyöreän reiän halkaisijan on kuitenkin oltava suurempi kuin fotonin koko. Mitä pienemmäksi pyöreä reikä tehdään, sitä lähemmäksi pääsemme fotonin tarkkaa sijaintia sen läpi kulkiessa. Emme kuitenkaan voi koskaan tietää, onko fotoni tuolloin epäkeskinen. Jos reikä on täsmälleen samankokoinen kuin fotoni, se ei kulje sen läpi. Kun reiän halkaisija pienenee, fotonin impulssi tai suunta sen poistuessa reiästä muuttuu yhä voimakkaammin.

Niels Bohr ja hänen kollegansa väittivät, että joudumme suuriin vaikeuksiin, jos oletamme, että asioista, jotka ovat liian pieniä nähdäksemme edes mikroskoopilla, pitää paikkansa kaikki se, mistä meillä on todisteita vain arkielämän mittakaavassa. Jokapäiväisessä elämässä asioilla on aina tietty sijainti. Atomien mittakaavassa meillä ei ole mitään todisteita, jotka tukisivat tätä päätelmää. Arkielämässä asioilla on tietty aika, jolloin ne tapahtuvat. Atomiasteikolla meillä ei ole todisteita tämän päätelmän tueksi. Jos jokapäiväisessä elämässä tarkkaillaan tehdasta ensimmäisen päivän yövuorosta toisen päivän päivävuoroon ja nähdään, kun valmis auto rullataan laivatelakalle, ei ole mitään järkeä sanoa, että on mahdotonta sanoa, onko auto toimitettu yövuoron vai päivävuoron aikana. Mutta atomiasteikolla voimme osoittaa tapauksia, joissa meidän on laskettava, että yksi fotoni on tuotettu kahtena ajankohtana. (Jos tämä ei ole tarpeeksi paha, voimme myös osoittaa tapauksia, joissa yksi fotoni on tuotettu kahdella vierekkäisellä laserilla.)

Osa vaikeudesta selvittää, mitä atomitasolla tapahtuu, on se, että haluaisimme tietää, missä jokin on ja mikä on sen liikerata, ja että haluaisimme tietää molemmat asiat samaan aikaan, mutta emme voi mitata sekä sijaintia että liikerataa samanaikaisesti. Joko mittaamme fotonin tai elektronin liikemäärän kerralla ja sen jälkeen mittaamme sen sijainnin ilman suurempaa viivettä kuin on tarpeen, tai sitten vaihdamme asioita ja mittaamme ensin sijainnin ja sitten liikemäärän. Ongelmana on se, että kun teemme ensimmäisestä mittauksesta melko varman (puristamalla sitä jollakin tavalla), lisäämme seuraavaan mittaukseen liittyvää epävarmuutta. Jos alkumittauksemme olisivat niin karkeat, että jokaisessa mittauksessa olisi paljon virhettä, voisimme parantaa asioita käyttämällä kevyempää kosketusta jokaisessa mittauksessa, mutta emme voisi koskaan päästä tietyn tarkkuusrajan yli.

Tiedämme jokapäiväisestä elämästä, että jos yritämme punnita jotakin pesukoneen päälle asetetulla kylpyhuoneen vaa'alla, kun pesukone on linkousvaiheessa, tulokset ovat epätarkkoja, koska vaa'an neula heiluu pahasti. Voimme sammuttaa pesukoneen. Mutta jos haluamme tehdä erittäin tarkkoja mittauksia, huomaamme, että naapurustossa ohi ajavat rekat saavat neulan heilumaan, joten voimme asettaa vaa'an jonkin päälle eristämään sen ulkopuolisilta häiriöiltä. Uskomme, että pystymme poistamaan värähtelyt tarpeeksi, jotta saamme juuri niin tarkat tulokset kuin haluamme. Emme koskaan ota huomioon, että vaa'alla oleva asia itse värähtelee tai että sillä on epämääräinen impulssi.

Jos päättelemme epävarmuusperiaatteesta taaksepäin, näyttää siltä, että minkään atomimittakaavan asian osalta ei itse asiassa ole olemassa varmaa sijaintia eikä varmaa vauhtia, ja että kokeilijat voivat pakottaa asiat määrittelemään ne vain epävarmuusperiaatteen asettamissa rajoissa. Bohr ja hänen kollegansa väittivät vain, että emme voi tietää mitään tekemättä mittauksia, ja kun mittauksia on tehty, voimme työntää asioita varmemman sijainnin tai varmemman impulssin suuntaan, mutta että emme voi saada aikaan absoluuttista lopullisuutta tai varmuutta, jota haluaisimme. Toiset kuitenkin ottivat tämän mahdollisuuden vakavasti ja väittivät, että jos matematiikka on oikeassa, niin ultrapienen maailman maailmassa ei voi olla varmuutta tai varmuutta. Tieteen luonteeseen kuuluu, että matematiikka on vain malli todellisuudesta, eikä ole mitään takeita siitä, että se on oikea malli.

Matematiikka ja sen ennustamien asioiden käytännön seuraukset ovat niin luotettavia, että niitä on hyvin vaikea kiistää, mutta matematiikan sanomaa todellisesta maailmasta on käsitelty monin eri tavoin. Niels Bohrin kanssa Kööpenhaminassa työskennelleiden tiedemiesten keskuudessa epävarmuusperiaatteen katsottiin tarkoittavan, että alkeistasolla fyysinen maailmankaikkeus ei ole olemassa deterministisessä muodossa. Se on pikemminkin kokoelma todennäköisyyksiä tai potentiaaleja.

Kööpenhaminan ryhmän matematiikan ympärille kietomaa tarinaa vasten on olemassa muitakin tarinoita, kuten "useiden universumien tulkinta", jonka mukaan aina kun kvanttiteorian mukaan on useita mahdollisia lopputuloksia, jokainen lopputulos tapahtuu omassa uudessa universumissaan. Einstein väitti, että ei ole olemassa useita mahdollisia lopputuloksia, joten on olemassa vain yksi maailmankaikkeus ja se on determinoitunut, tai kuten hän asian ilmaisi, "Jumala ei noppaa".

 
Jos h olisi pienin mahdollinen energiamäärä, perusyhtälö, joka osoittaa eri taajuisten fotonien sisältämän energian, ei olisi tasapainossa. Se olisi väärin.  

Epävarmuusperiaatetta vastaan esitetyt vastaväitteet

Albert Einstein näki, että uusi kvanttimekaniikka merkitsi sijainnin ja liikemäärän puuttumista mittauksia edeltävältä ajalta, ja hän vastusti sitä voimakkaasti. Hän uskoi vakaasti siihen, että asioilla oli ennen mittauksia määrätyt sijainnit ja määrätyt momentit ja että se, että mittaamalla yhtä parin asioista ja häiritsemällä mahdollisuutta mitata tarkasti toista, ei puhu sen puolesta, että jompikumpi niistä puuttuisi ennen mittauksia. Hän ja kaksi hänen kollegaansa kirjoittivat "EPR-paperina" tunnetun teoksen. Kyseisessä paperissa väitetään, että on oltava ominaisuuksia, jotka määrittävät sijainnin ja liikemäärän, ja että jos voisimme nähdä ne tai jos voisimme saada tietoa niistä, voisimme matemaattisesti tietää ja ennustaa sijainnin ja liikemäärän. Pitkään ajateltiin, että ei ole mitään keinoa todistaa tai kumota sitä, mikä oli Einsteinille uskonkappale. Väite oli hyvin hedelmällinen, koska se johti kaikkeen nykyaikaiseen kietoutumisen kehitykseen.

Matemaattisesti Einstein on osoittautunut vääräksi. John Stewart Bell kehitti vuonna 1964 matemaattisen menetelmän, jolla voitiin erottaa toisistaan kahden hiukkasen käyttäytyminen, joilla on määrätyt tilat, jotka ovat vain tuntemattomia kahdelle niitä tutkivalle henkilölle, ja kahden hiukkasen käyttäytyminen, joilla on kietoutuneet tilat, jotka ovat määrittelemättömiä tai epävarmoja, kunnes ne mitataan. Hänen menetelmänsä osoittaa, että todennäköisyydet tiettyjen tulosten saamiseksi ovat erilaiset näissä kahdessa eri oletuksessa. Hänen työtään kutsutaan Bellin teoreemaksi tai Bellin epätasa-arvoksi. Kokeet ovat osoittaneet, että luonto käyttäytyy Bellin kuvaamalla tavalla.

 

Toinen reitti epävarmuuteen

Heisenbergin epävarmuusperiaatetta koskevat ensimmäiset keskustelut perustuivat malliin, jossa ei otettu huomioon, että elektronien, protonien jne. kaltaisilla ainehiukkasilla on aallonpituus. Vuonna 1926 Louis de Broglie osoitti, että kaikilla asioilla, ei vain fotoneilla, on oma taajuutensa. Asioilla on sekä aalto- että hiukkasluonne, aivan kuten fotoneillakin. Jos yritämme tehdä protonin kaltaisen esineen aallosta kapeamman ja korkeamman, se selkeyttäisi sen sijaintia, mutta silloin momentti muuttuisi huonommin määritellyksi. Jos yritämme tehdä aaltokuvauksen impulssiosasta selkeämmän eli saada sen pysymään kapeammalla arvoalueella, silloin aallon huippu leviää ja sen sijainnista tulee epämääräisempi.

Aalto, joka on osa fotonin kuvausta, ei ole kvanttimekaniikassa samanlainen asia kuin aalto valtameren pinnalla tai ääniaaltojen muodostamat paineistetun ja laimennetun ilman alueet. Sen sijaan näillä aalloilla on huippuja tai suuren amplitudin alueita, jotka liittyvät todennäköisyyteen löytää jotain kyseisessä pisteessä tilassa ja ajassa. Tarkemmin sanottuna amplitudin neliö antaa todennäköisyyden jonkin ilmiön esiintymiselle.

Fotoniin kohdistuva aalto voi olla puhdas siniaalto. Tällöin jokaisen huippuarvon neliö antaisi todennäköisyyden havaita fotoni kyseisessä pisteessä. Koska siniaaltojen amplitudit ovat kaikkialla samat, todennäköisyys havaita fotoni jokaisessa pisteessä olisi sama. Käytännössä siis yhden fotonin aallon tunteminen ei antaisi vihjeitä siitä, mistä sitä pitäisi etsiä. Toisaalta fotonin impulssi liittyy matemaattisesti sen aallon amplitudiin. Koska tässä tapauksessa kyseessä on puhdas siniaalto, aallon jokaisen jakson amplitudi on sama, ja siksi tähän aaltoon liittyy vain yksi momentin arvo. Emme tietäisi, mihin fotoni osuisi, mutta tietäisimme tarkalleen, kuinka kovaa se osuisi.

Valonsäteissä, jotka keskittyvät johonkin havaintoruudun pisteeseen, fotoneihin liittyvät aallot eivät ole puhtaita siniaaltoja. Sen sijaan ne ovat aaltoja, joilla on suuri amplitudi yhdessä pisteessä ja paljon pienemmät amplitudit tämän korkeimman huipun molemmin puolin. Matemaattisesti on mahdollista analysoida tällainen aalto useiksi erilaisiksi siniaalloiksi, joilla on eri aallonpituudet. On hieman helpompaa havainnollistaa tämän prosessin kääntöpuolta tarkastelemalla alkuperäistä siniaaltoa, jolla on yksi taajuus ja johon lisätään toinen siniaalto, jolla on eri aallonpituus, sitten kolmas, sitten neljäs ja niin edelleen. Tuloksena on monimutkainen aalto, jossa on yksi korkea huippu ja joka sisältää suuren määrän aaltoja, joiden aallonpituus on erilainen ja siten myös momentti. Tällöin todennäköisyys, että fotoni ilmestyy tiettyyn pisteeseen, on erittäin suuri, mutta sen välittämä impulssi voi osoittautua riippuvaiseksi minkä tahansa komponenttiaallon aallonpituudesta. Toisin sanoen arvo p = ħ/λ ei ole enää yksi ainoa arvo, koska kaikki koottujen "aallonpituudeltaan eripituisten aaltojen" pituudet on otettava huomioon.

Simulaatio osoittaa, miten hiukkasen sijainnin terävöitymistä voidaan mallintaa matemaattisesti: Aseta monia erilaisia aaltomuotoja alkuperäisen siniaallon päälle. Keskipiste muodostaa yhä korkeamman ja korkeamman piikin, ja muiden piikkien määrä lisääntyy mutta niiden korkeus pienenee, koska ne häiritsevät toisiaan. Loppujen lopuksi superpositiossa on siis monia erilaisia aaltoja, joista jokaisella on erilainen aallonpituus ja (p = ħ/λ) erilainen impulssi, mutta vain yksi hyvin korkea huippu, joka kasvaa korkeammaksi ja kapeammaksi ja antaa meille jotain yhä lähempänä ja lähempänä määrättyä sijaintia.

Jotta vauhti olisi yhä selkeämpi, meidän olisi poistettava yhä enemmän päällekkäisiä siniaaltoja, kunnes jäljelle jäisi vain yksinkertainen siniaalto. Näin tehdessämme pienentäisimme asteittain keskihuipun korkeutta ja kasvattaisimme asteittain niiden kilpailevien paikkojen korkeutta, joissa hiukkanen voisi olla.

Kun aloitamme subatomisten hiukkasten aaltokuvan, käsittelemme tyypillisesti aina tapauksia, joissa on suhteellisen korkeat keskihuiput ja suhteellisen monta komponentin aallonpituutta. Näissä olosuhteissa ei koskaan voida ennustaa tarkkaa sijaintia tai tarkkaa impulssia. Jos matemaattinen malli on tarkka kuvaus todellisesta maailmasta, millään fotonilla tai muulla subatomisella hiukkasella ei ole tarkkaa sijaintia eikä varmaa impulssia. Kun mittaamme tällaista hiukkasta, voimme valita menetelmän, joka puristaa piikkiä entisestään ja tekee siitä kapeamman, tai voimme valita menetelmän, joka laskee piikkiä ja tasoittaa komponenttien aallonpituudet. Riippuen siitä, mitä mittaamme ja miten mittaamme sen, voimme saada sijaintimme selvemmäksi tai voimme saada impulssialueemme kapeammaksi. Voimme huolehtia kokeen suunnittelussa siitä, että vältämme erilaisia tapoja horjuttaa laitetta, mutta emme pääse eroon siitä, että alun perin mikään ei ollut täysin varmaa.

 
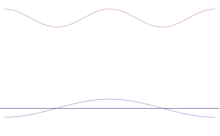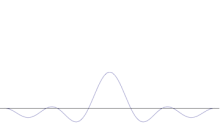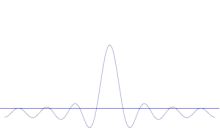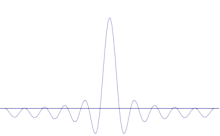
Useiden tasoaaltojen superpositio. Aaltopaketti paikallistuu yhä enemmän, kun siihen lisätään useita aaltoja. Fourier-muunnos on matemaattinen operaatio, joka jakaa aaltopaketin yksittäisiin tasoaaltoihin. Huomaa, että tässä esitetyt aallot ovat reaalisia vain havainnollistamistarkoituksessa, kun taas kvanttimekaniikassa aaltofunktio on yleensä kompleksinen.  

Kulttuurivaikutteet

Heisenbergin epävarmuusperiaate on vaikuttanut suuresti vapaata tahtoa koskeviin väitteisiin. Klassisen fysiikan teorioiden mukaan on mahdollista väittää, että syyn ja seurauksen lait ovat vääjäämättömiä ja että kun maailmankaikkeus on kerran alkanut tietyllä tavalla, kaiken aineen ja energian vuorovaikutukset, jotka tapahtuvat tulevaisuudessa, voidaan laskea tuosta alkutilanteesta. Koska kaikki on ehdottomasti seurausta siitä, mitä sitä ennen tapahtui, he väittivät, että jokainen päätös, jonka ihminen tekee, ja jokainen tilanne, johon ihminen joutuu, oli ennalta määrätty ajan alusta lähtien. Meillä ei siis ole valinnanvaraa siinä, mitä teemme.

Vapaaseen tahtoon uskovat väittävät, että kvanttimekaniikan lait eivät ennusta, mitä tulee tapahtumaan, vaan ainoastaan sen, mikä on todennäköisempää ja mikä epätodennäköisempää. Siksi jokainen teko on satunnaisten "kolikonheiton" tulos, eikä mitään päätöstä voida jäljittää tiettyihin välttämättömiin ennakkoedellytyksiin.

Ilmaisuista "kvanttihyppy" ja "kvanttihyppy" on tullut tavallisia tapoja puhua asioista. Tavallisesti ihmisten tarkoituksena on kuvata jotakin asiaa niin, että siihen liittyy valtava muutos, joka tapahtuu lyhyessä ajassa. Itse asiassa termi viittaa siihen, miten elektroni käyttäytyy atomissa joko silloin, kun se absorboi ulkopuolelta tulevan fotonin ja hyppää siten yhdeltä radalta atomin ytimen ympärillä korkeammalle radalle, tai silloin, kun se lähettää fotonin ja putoaa siten korkeammalta radalta alemmalle radalle. Niels Bohrin ja hänen kollegoidensa ajatuksena oli, että elektroni ei liiku kiertoradalta toiselle, vaan se katoaa yhdeltä kiertoradalta ja ilmestyy välittömästi toiselle kiertoradalle. Kvanttihyppy ei siis todellakaan ole mikään maailmaa järisyttävä muutos, vaan äkillinen pieni muutos.

Kun ihminen mittaa jotakin prosessia subatomisella mittakaavalla ja epävarmuusperiaate ilmenee, ihmisen toiminnan voidaan sanoa vaikuttaneen mitattavaan asiaan. Mittauksen tekeminen, jonka tarkoituksena on saada varma tieto hiukkasen sijainnista, vaikuttaa väistämättä sen liikemäärään, ja mitä tahansa tehdäänkin liikemäärän mittaamiseksi mahdollisimman pian sen sijainnin mittaamisen jälkeen, todennäköisyydet siitä, mikä liikemäärä havaitaan, eivät voi olla muuttumatta. Epävarmuusperiaate voi siis selittää eräitä tutkijoiden tuottamia häiriöitä, jotka vaikuttavat kokeen tai havainnon tuloksiin. Kaikki havainnointivaikutukset eivät kuitenkaan johdu kvanttivaikutuksista tai epävarmuusperiaatteesta. Loput ovat "havaitsijan vaikutuksia" mutta eivät kvanttiepävarmuusvaikutuksia.

Tarkkailuvaikutukset sisältävät kaikenlaisia asioita, jotka toimivat tavallisessa inhimillisessä tapahtumamittakaavassa. Jos antropologi yrittää saada selkeän käsityksen elämästä primitiivisessä yhteiskunnassa, mutta hänen läsnäolonsa järkyttää yhteisöä, jossa hän vierailee, hänen tekemänsä havainnot voivat olla hyvin harhaanjohtavia. Mikään asiaankuuluvista vuorovaikutuksista ei kuitenkaan tapahdu kvanttimekaniikan tai epävarmuusperiaatteen kuvaamalla tasolla.

Joskus sanaa "kvantti" käytetään mainostarkoituksessa osoittamaan jotain uutta ja tehokasta. Esimerkiksi pienten bensiinimoottoreiden valmistajalla Briggs and Strattonilla on bensiinikäyttöisiin ruohonleikkureihin ja vastaaviin puutarhatyökaluihin tarkoitettuja nelisylinterisiä pienitehoisia moottoreita, joita se kutsuu nimellä "Quantum".

 

Lisää lukemista

• Introducing Quantum Theory, s. 115 ja s. 158.

J.P. McEvoy ja Oscar Zarate