Planckin vakio | Se on nimetty fyysikko Max Planckin mukaan

Tausta

Tässä artikkelissa käytetyt symbolit.
Symboli Merkitys E Energia h Planckin vakio k Boltzmannin vakio c valon nopeus λ säteilyn aallonpituus ν säteilytaajuus T absoluuttinen lämpötila

Vuosina 1670-1900 tutkijat keskustelivat valon luonteesta. Jotkut tiedemiehet uskoivat, että valo koostuu miljoonista pienistä hiukkasista. Toiset tutkijat uskoivat, että valo oli aalto.

Valo: aaltoja vai hiukkasia?

Christiaan Huygens kirjoitti vuonna 1678 kirjan Traité de la lumiere ("Tutkielma valosta"). Hän uskoi, että valo koostuu aalloista. Hänen mukaansa valo ei voinut koostua hiukkasista, koska kahden säteen valo ei kimpoile toisistaan. Vuonna 1672 Isaac Newton kirjoitti kirjan Opticks. Hän uskoi, että valo koostuu punaisista, keltaisista ja sinisistä hiukkasista, joita hän kutsui korpuksiksi. Newton selitti tämän "kahden prisman kokeella". Ensimmäinen prisma hajotti valon eri väreihin. Toinen prisma yhdisti nämä värit takaisin valkoiseksi valoksi.

1700-luvulla Newtonin teoriaan kiinnitettiin eniten huomiota. Vuonna 1803 Thomas Young kuvasi "kaksoisrakokokeen". Tässä kokeessa kahden kapean raon läpi kulkeva valo interferoi itsensä kanssa. Tämä aiheuttaa kuvion, joka osoittaa, että valo koostuu aalloista. Valon aaltoteoriaan kiinnitettiin eniten huomiota 1800-luvun loppupuolella. James Clerk Maxwell kehitti 1860-luvulla yhtälöt, jotka kuvasivat sähkömagneettista säteilyä aaltoina.

Sähkömagneettisen säteilyn teoriassa valoa, radioaaltoja, mikroaaltoja ja monia muita aaltotyyppejä pidetään samoina asioina, paitsi että niillä on eri aallonpituudet. Silmillämme näkyvän valon aallonpituus on noin 400-600 nm. Radioaaltojen aallonpituus vaihtelee 10 metristä 1500 metriin, ja mikroaaltojen aallonpituus on noin 2 cm. Tyhjiössä kaikki sähkömagneettiset aallot kulkevat valon nopeudella. Sähkömagneettisen aallon taajuus saadaan:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Symbolit määritellään tässä.

Mustat runkopatterit

Kaikki lämpimät asiat säteilevät lämpösäteilyä, joka on sähkömagneettista säteilyä. Useimmilla maapallolla olevilla asioilla tämä säteily on infrapuna-aluetta, mutta jos jokin asia on hyvin kuuma (1000 °C tai enemmän), se säteilee näkyvää säteilyä eli valoa. Monet tutkijat tutkivat 1800-luvun lopulla mustan kappaleen säteilijöiden sähkömagneettisen säteilyn aallonpituuksia eri lämpötiloissa.

Rayleigh-Jeansin laki

Lordi Rayleigh julkaisi Rayleigh-Jeansin lain perusteet ensimmäisen kerran vuonna 1900. Teoria perustui kaasujen kineettiseen teoriaan. Sir James Jeans julkaisi täydellisemmän teorian vuonna 1905. Laki suhteuttaa mustan kappaleen säteilijän eri lämpötiloissa luovuttaman sähkömagneettisen energian määrän ja aallonpituuden. Tätä kuvaava yhtälö on:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

Pitkän aallonpituuden säteilyn osalta tämän yhtälön ennustamat tulokset vastasivat hyvin laboratoriossa saatuja käytännön tuloksia. Lyhyillä aallonpituuksilla (ultraviolettivalo) teorian ja käytännön välinen ero oli kuitenkin niin suuri, että se sai lempinimen "ultraviolettikatastrofi".

Planckin laki

Wien julkaisi vuonna 1895 mustan kappaleen säteilyä koskevien tutkimustensa tulokset. Hänen kaavansa oli:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Tämä kaava toimi hyvin lyhytaaltoiselle sähkömagneettiselle säteilylle, mutta se ei toiminut hyvin pitkillä aallonpituuksilla.

Vuonna 1900 Max Planck julkaisi tutkimustensa tulokset. Hän yritti kehittää mustan kappaleen säteilyä koskevan lausekkeen, joka ilmaistaisiin aallonpituutena, olettamalla, että säteily koostuu pienistä kvanteista, ja sen jälkeen katsomalla, mitä tapahtuisi, jos kvanteista tehtäisiin äärettömän pieniä (tämä on tavanomainen matemaattinen lähestymistapa). Lauseke oli seuraava:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}} .

Jos valon aallonpituuden annetaan kasvaa hyvin suureksi, voidaan osoittaa, että Raleigh-Jeansin ja Planckin suhteet ovat lähes identtiset.

Hän laski h:n ja k:n ja totesi, että

h = 6,55×10⁻²⁷ erg-sek.

k = 1,34×10⁻¹⁶ erg-deg .^-1

Arvot ovat lähellä nykyisin hyväksyttyjä arvoja 6,62606×10⁻³⁴ ja 1,38065×10⁻¹⁶ . Planckin laki sopii hyvin yhteen kokeellisten tietojen kanssa, mutta sen täysi merkitys ymmärrettiin vasta useita vuosia myöhemmin.

Valon kvanttiteoria

On käynyt ilmi, että valosähköinen ilmiö irrottaa elektroneja, jos valo saavuttaa tietyn kynnystaajuuden. Tämän alapuolella metallista ei voi emittoitua elektroneja. Albert Einstein julkaisi vuonna 1905 artikkelin, jossa hän selitti ilmiön. Einstein esitti, että valonsäde ei ole avaruudessa etenevä aalto, vaan pikemminkin kokoelma erillisiä aaltopaketteja (fotoneja), joilla kullakin on energiaa. Einsteinin mukaan ilmiö johtui siitä, että fotoni osui elektroniin. Tämä osoitti valon hiukkasluonteen.

Einstein havaitsi myös, että pitkän aallonpituuden omaavalla sähkömagneettisella säteilyllä ei ollut vaikutusta. Einsteinin mukaan tämä johtui siitä, että "hiukkasilla" ei ollut tarpeeksi energiaa häiritäkseen elektroneja.

Planck esitti, että jokaisen fotonin energia on yhteydessä fotonin taajuuteen Planckin vakion avulla. Tämä voidaan kirjoittaa matemaattisesti seuraavasti:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Planck sai Nobel-palkinnon vuonna 1918 tunnustuksena hänen fysiikan edistämispalveluksistaan, jotka hän oli tehnyt energiakvanttien löytämisellä. Vuonna 1921 Einstein sai Nobelin palkinnon siitä, että hän yhdisti Planckin vakion valosähköiseen ilmiöön.

 
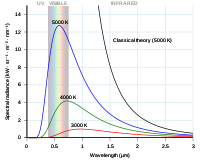
Rayleigh-Jeansin käyrä ja Planckin käyrä piirrettyinä fotonin aallonpituuden suhteen.  


Solwayn konferenssi 1911. Planck, Einstein ja Jeans seisovat. Planck on toinen vasemmalta. Einstein on toinen oikealta. Jeans on viides oikealta. Wien istuu, kolmas oikealta.  


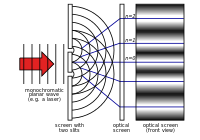
Youngin kaksoisrakokoe  


Kuvitus on otettu Newtonin alkuperäisestä kirjeestä Royal Societylle (1. tammikuuta 1671 [juliaaninen kalenteri]). S tarkoittaa auringonvaloa. Tasojen BC ja DE välinen valo on värillinen. Nämä värit yhdistyvät uudelleen muodostaen auringonvalon tasolle GH.  

Sovellus

Planckin vakio on tärkeä monissa sovelluksissa. Seuraavassa luetellaan muutamia niistä.

Bohrin atomimalli

Vuonna 1913 Niels Bohr julkaisi Bohrin mallin atomin rakenteesta. Bohrin mukaan ytimen ympärillä liikkuvien elektronien kulmavauhdilla voi olla vain tiettyjä arvoja. Nämä arvot saadaan yhtälöstä

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

jossa

L = tasoon liittyvä kulmamomentti.

n = positiivinen kokonaisluku.

h = Planckin vakio.

Bohrin atomimallin avulla voidaan laskea elektronien energia kullakin tasolla. Elektronit täyttävät tavallisesti atomin alimmat tilat. Jos atomi saa energiaa esimerkiksi sähkövirrasta, elektronit virittyvät korkeampaan tilaan. Tämän jälkeen elektronit putoavat takaisin alempaan tilaan ja menettävät ylimääräisen energiansa lähettämällä fotonin. Koska energiatasoilla on tietyt arvot, myös fotoneilla on tietyt energiatasot. Näin emittoitunut valo voidaan jakaa eri väreihin käyttämällä prismaa. Jokaisella alkuaineella on oma kuvionsa. Neonin kuvio on esitetty vieressä.

Heisenbergin epävarmuusperiaate

Vuonna 1927 Werner Heisenberg julkaisi epävarmuusperiaatteen. Periaatteen mukaan mittausta ei ole mahdollista tehdä häiritsemättä mitattavaa asiaa. Se asettaa myös rajan mittauksen tekemisen aiheuttamalle pienimmälle häiriölle.

Makroskooppisessa maailmassa näillä häiriöillä on hyvin vähän merkitystä. Jos esimerkiksi mitataan nestepullon lämpötilaa, lämpömittari absorboi pienen määrän energiaa lämmetessään. Tämä aiheuttaa pienen virheen lopulliseen lukemaan, mutta tämä virhe on pieni eikä sillä ole merkitystä.

Kvanttimekaniikassa asiat ovat toisin. Jotkin mittaukset tehdään tarkastelemalla sironneiden fotonien kuvioita. Yksi tällainen esimerkki on Comptonin sironta. Jos mitataan sekä hiukkasen sijaintia että impulssia, epävarmuusperiaatteen mukaan impulssin mittaustarkkuuden ja sijainnin mittaustarkkuuden välillä on kompromissi. Yhtälö, joka kuvaa tätä kompromissia, on seuraava:

Δ x Δ p ⩾ h 4 π {\displaystyle \Delta x\,\Delta p\geqslant {\frac {h}{4\pi }\qquad \qquad \qquad \qquad }

jossa

Δp = impulssin epävarmuus.

Δx = sijainnin epävarmuus.

h = Planckin vakio.

Valodiodien väri

Oikealla olevassa sähköpiirissä jännitehäviö valodiodin (LED) yli riippuu LEDin materiaalista. Piidiodien jännitehäviö on 0,6 V. LEDien jännitehäviö on kuitenkin 1,8-2,7 V. Tämän tiedon avulla käyttäjä voi laskea Planckin vakion.

Energia, jonka yksi elektroni tarvitsee hyppäämään LED-materiaalin potentiaaliesteen yli, saadaan seuraavalla kaavalla

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

jossa

Q_e on yhden elektronin varaus.

V_L on jännitehäviö ledin yli.

Kun elektroni hajoaa takaisin, se lähettää yhden valofotonin. Fotonin energia saadaan samasta yhtälöstä, jota käytetään valosähköisessä ilmiössä. Jos nämä yhtälöt yhdistetään, valon aallonpituus ja jännite liittyvät toisiinsa seuraavasti

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}\,}

Tämän suhteen perusteella voidaan laskea alla oleva taulukko.

Väri	Aallonpituus (nm)	Jännite
punainen valo	650	1.89
vihreä valo	550	2.25
sininen valo	470	2.62

 
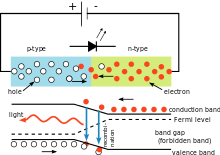
Yksinkertainen LED-piiri, joka havainnollistaa Planckin vakion käyttöä. Lähtevän valon väri riippuu diodin jännitehäviöstä. Valon aallonpituus voidaan laskea Planckin vakion avulla.  


Neonin näkyvä spektri. Jokainen viiva edustaa eri energiatasoparia.  


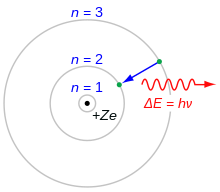
Bohrin atomimalli. Elektroni, joka putoaa n=3-kuoresta n=2-kuoreen, menettää energiaa. Tämä energia kulkeutuu pois yksittäisenä fotonina.  

Planckin vakion arvo ja kilogramman uudelleenmääritelmä

Sen löytämisen jälkeen h:n mittaukset ovat parantuneet huomattavasti. Planck ilmoitti ensimmäisen kerran h:n arvoksi 6,55 × 10⁻²⁷ erg-sek. Tämä arvo on 5 prosentin sisällä nykyisestä arvosta.

Maaliskuun 3. päivänä 2014 paras mitattu h SI-yksiköissä on 6,62606957×10⁻³⁴ J-s. Vastaava luku cgs-yksiköissä on 6,62606957×10⁻²⁷ erg-sek. H:n suhteellinen epävarmuus on 4,4×10 . ⁻⁸

Pelkistetty Planckin vakio (ħ) on arvo, jota käytetään joskus kvanttimekaniikassa. Se määritellään seuraavasti

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Planckin yksiköitä käytetään joskus kvanttimekaniikassa SI-yksikön sijasta. Tässä järjestelmässä pelkistetyn Planckin vakion arvo on 1, joten Planckin vakion arvo on 2π.

Plancksin vakio voidaan nyt mitata erittäin tarkasti. Tämä on saanut BIPM:n harkitsemaan uutta kilogramman määritelmää. Kansainvälistä kilogramman prototyyppiä ei enää käytetä kilogramman määrittelyssä. Sen sijaan BIPM määrittelee Planckin vakiolle tarkan arvon. Tutkijat käyttävät tätä arvoa sekä metrin ja sekunnin määritelmiä kilogramman määrittelyyn.

 

Teoreettisen Planckin vakion arvo

Planckin vakio voidaan johtaa myös matemaattisesti:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}}{[0.9163a_{0}]}^{2}]^{2}}}{f_{1r}}}^{5} \cdot {s}=6.63\times 10^{-34}J\cdot s}

Tässä μ 0 {\displaystyle \mu _{0}} on vapaan tilan permeabiliteetti, c {\displaystyle c} on valon nopeus, q 0 {\displaystyle q_{0}} on elektronin sähkövaraus, a 0 {\displaystyle a_{0}} on Bohrin säde, ja f 1 r {\displaystyle f_{1r}} on elektronin kiertotaajuus vetyatomissa ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} . Kun nämä vakioarvot korvataan teoreettiseen Planckin vakioon, teoreettinen Planckin vakion arvo on täsmälleen sama kuin kokeellinen arvo.

 Planckin vakion alkeiskaava protonin ja elektronin massasuhteen, elektronin varauksen, valonnopeuden ja tyhjiön permittiivisyyden avulla on johdettu seuraavassa. Se ilmaistaan seuraavasti:

h = e 2 c ε 0 π 2 3 m p m e {\displaystyle h={\frac {e^{2}}{c\,\varepsilon _{0}}}{\sqrt {\pi \,{\sqrt {\frac {2}{3}}}\,\,{\frac {m_{p}}{m_{e}}}}}}

jossa e {\displaystyle e} on elektronin alkeisvaraus, m p {\displaystyle m_{p}} protonin massa, m e {\displaystyle m_{e}} elektronin massa, ε 0 {\displaystyle \varepsilon _{0}}} tyhjiön permittiivisyys ja c {\displaystyle c} valon nopeus.

 

Aiheeseen liittyvät sivut

• Aalto-hiukkasdualismi