Heisenbergin epävarmuusperiaate – selitys, merkitys ja esimerkit

Hämmennys tarkkailijan vaikutuksen kanssa

Historiallisesti epävarmuusperiaate on sekoitettu fysiikassa esiintyvään hieman samankaltaiseen vaikutukseen, jota kutsutaan tarkkailijavaikutukseksi. Sen mukaan joidenkin järjestelmien mittauksia ei voida tehdä vaikuttamatta järjestelmiin. Heisenberg tarjosi tällaista kvanttitason tarkkailijavaikutusta kvanttiepävarmuuden fysikaaliseksi "selitykseksi".

Nyt on kuitenkin selvää, että epävarmuusperiaate on kaikkien aaltomuotoisten järjestelmien ominaisuus. Se syntyy kvanttimekaniikassa yksinkertaisesti kaikkien kvanttikohteiden aineen aaltoluonteesta johtuen. Näin ollen epävarmuusperiaate itse asiassa ilmaisee kvanttisysteemien perustavanlaatuisen ominaisuuden, eikä se ole väite nykyisen teknologian havaintomenestyksestä. "Mittauksella" ei tarkoiteta vain prosessia, johon fyysikko-tarkkailija osallistuu, vaan pikemminkin mitä tahansa vuorovaikutusta klassisten ja kvanttiobjektien välillä tarkkailijasta riippumatta.

Määrittelemättömyyden ajatus

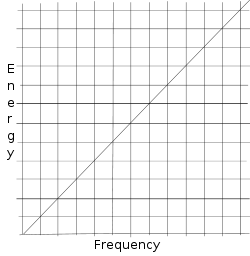
Epävarmuusperiaate on peräisin Werner Heisenbergin matriisimekaniikasta. Jo Max Planck tiesi, että valoyksikön energia on verrannollinen valoyksikön taajuuteen ( E ∝ ν {\displaystyle E\propto \nu } ) ja että sen energiamäärä voidaan ilmaista tutuilla termeillä, kuten joule, käyttämällä suhteellisuusvakiota. Hänen maailmalle antamaa vakiota kutsutaan nykyään Planckin vakioksi, ja sitä edustaa kirjain h. Kun kvanttimekaniikan ilmaisemiseen käytetään matriiseja, usein kaksi matriisia on kerrottava keskenään, jotta saadaan kolmas matriisi, joka antaa vastauksen, jota fyysikko yrittää löytää. Mutta kertomalla matriisi, kuten P (impulssi), matriisilla, kuten X (asento), saadaan eri vastausmatriisi kuin kertomalla X:llä P:llä. Tulos, joka saadaan kertomalla P X:llä ja X P:llä, ja vertaamalla niitä keskenään, sisältää aina Planckin vakion tekijänä. Planckin vakion kirjoittamiseen käytettävä luku riippuu aina käytettävästä mittausjärjestelmästä. (Tietyssä mittausjärjestelmässä sen lukuarvo on yksi.) Myös oikealla olevassa kaaviossa olevan, taajuuden ja energian suhdetta kuvaavan viivan kaltevuus riippuu valitusta mittausjärjestelmästä.

Seuraavat kaaviot osoittavat, mitä tapahtuu, kun yritämme mitata sekä sijaintia että vauhtia.

Tämän matemaattisen havainnon käytännön tulos on, että kun fyysikko tekee sijainnin selvemmäksi, impulssi muuttuu vähemmän selväksi, ja kun fyysikko tekee impulssin selvemmäksi, sijainti muuttuu vähemmän selväksi. Heisenberg sanoi, että asiat ovat "epämääräisiä", ja muut sanoivat mielellään, että ne ovat "epävarmoja". Mutta matematiikka osoittaa, että maailmassa olevat asiat ovat epämääräisiä tai "epäselviä", eivätkä vain ihmiset ole epävarmoja siitä, mitä tapahtuu.

Määräämättömyyden saattaminen matemaattiseen muotoon

Tässä esitellään ensimmäinen yhtälö, joka antoi perusajatuksen, joka myöhemmin ilmeni Heisenbergin epävarmuusperiaatteessa.

Heisenbergin uraauurtavassa artikkelissa vuodelta 1925 ei käytetä eikä edes mainita matriiseja. Heisenbergin suuri menestys oli "järjestelmä, jolla pystyttiin periaatteessa määrittelemään yksiselitteisesti vetysateilun olennaiset fysikaaliset ominaisuudet (siirtymätaajuudet ja amplitudit)".

Kun Heisenberg oli kirjoittanut läpimurtopaperinsa, hän antoi sen yhdelle opettajistaan korjattavaksi ja lähti lomalle. Max Born oli ymmällään yhtälöistä ja ei-kommutoivista yhtälöistä, joita jopa Heisenberg piti ongelmana. Useiden päivien kuluttua Born tajusi, että nämä yhtälöt olivat ohjeita matriisien kirjoittamiseen. Matriisit olivat uusia ja outoja jopa silloisille matemaatikoille, mutta se, miten niillä voi tehdä matematiikkaa, oli jo selvästi tiedossa. Hän ja muutama muu selvittivät kaiken matriisimuodossa ennen kuin Heisenberg palasi lomaltaan, ja muutaman kuukauden kuluessa uusi kvanttimekaniikka matriisimuodossa antoi heille pohjan toiselle paperille.

Max Born näki, että kun pq:ta ja qp:tä edustavat matriisit lasketaan, ne eivät ole yhtä suuria. Heisenberg oli jo nähnyt saman asian alkuperäisen kirjoitustapansa perusteella, ja Heisenberg saattoi arvata sen, mikä oli Bornille lähes välittömästi selvää - että pq:n ja qp:n vastausmatriisien välinen ero sisältäisi aina kaksi tekijää, jotka tulivat Heisenbergin alkuperäisestä matematiikasta: Planckin vakio h ja i, joka on negatiivisen ykkösen neliöjuuri. Heisenbergin alkuperäisiin yhtälöihin oli siis piilotettu ajatus siitä, mitä Heisenberg kutsui mieluummin "määrittelemättömyysperiaatteeksi" (joka tunnetaan yleensä epävarmuusperiaatteena).

Heisenberg oli tutkinut muutoksia, jotka tapahtuvat atomissa, kun elektroni vaihtaa energiatasoaan ja siten siirtyy lähemmäs atomin keskipistettä tai kauemmas sen keskipisteestä, ja erityisesti tilanteita, joissa elektroni putoaa alempaan energiatilaan kahdessa vaiheessa. Max Born selitti, miten hän käytti Heisenbergin outoa "reseptiä" atomin energiatasolta n energiatasolle n-b tapahtuvan muutoksen tulon C löytämiseksi, mikä tarkoitti sitä, että hän otti summan, joka saadaan kertomalla yksi muutos jossakin nimeltä A (joka voi olla esimerkiksi jonkin fotonin taajuus), joka aiheutuu atomissa olevan elektronin energiamuutoksesta energiatilasta n energiatilaan n-a, seuraavalla muutoksella jossakin nimeltä B (joka voi olla esimerkiksi muutoksen amplitudi), joka aiheutuu toisesta energiatilan muutoksesta energiatilasta n-a energiatilaan n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

ja löysin jotain mullistavaa:

Tarkastelemalla ...esimerkkejä...[Heisenberg] löysi tämän säännön..... Tämä tapahtui kesällä 1925. Heisenberg...otti virkavapaata...ja luovutti paperinsa minulle julkaistavaksi.....

Heisenbergin kertolaskusääntö ei jättänyt minulle rauhaa, ja viikon intensiivisen pohdinnan ja kokeilun jälkeen muistin yhtäkkiä algebrallisen teorian....Tällaiset kvadraattiset matriisit ovat matemaatikoille varsin tuttuja, ja niitä kutsutaan matriiseiksi, ja niihin liittyy tietty kertolaskusääntö. Sovelsin tätä sääntöä Heisenbergin kvanttiehtoihin ja huomasin, että se sopi diagonaalielementtien osalta. Oli helppo arvata, mitä muiden elementtien oli oltava, nimittäin nolla, ja heti edessäni seisoi outo kaava nimeltä

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
 [Symboli Q on siirtymän matriisi, P on impulssimatriisi, i tarkoittaa negatiivisen ykkösen neliöjuurta ja h on Planckin vakio].

Myöhemmin Heisenberg muotoili löytönsä toiseen matemaattiseen muotoon:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Erikoismerkkiä ℏ {\displaystyle {\hbar }} kutsutaan nimellä "h-bar" tai "redusoitu Planksin vakio", ja se on yhtä suuri kuin h 2 π {\displaystyle {\frac {h}{2\pi }}} . )

Matematiikka on tapa kuvata reaalimaailmassa tapahtuvia asioita. Voisit kuvitella, että olisi helppoa saada samanaikaisesti sekä jonkin asian tarkka sijainti että sen tarkka massa, liikerata ja nopeus. Todellisuudessa sinun on kuitenkin tehtävä kaksi asiaa saadaksesi vastauksen. Jos mittaat jonnekin suuren vuoren jyrkänteeseen juuttuneen luodin sijaintia ja vauhtia, asia on yksinkertainen. Vuori ei näytä menevän minnekään, eikä luoti myöskään. Joten sen sijainti tiedetään ja sen nopeus on 0, joten sen impulssi on myös 0. Mutta jos luoti on jossain aseen ja kohteen välissä, sen sijaintia on vaikea saada selville millään hetkellä. Parasta, mitä voimme ehkä tehdä, on ottaa siitä kuva käyttämällä kameraa, jossa on hyvin nopea suljin. Mutta yksi ainoa sulkimen painallus antaisi vain yhden asian, luodin sijainnin hetkellä t. Saadaksemme vauhtia voisimme laittaa luodin tielle parafiinipalikan ja mitata, miten parafiinipalikka liikkui, kun se pysäytti luodin. Tai jos tiedämme luodin massan, voimme ottaa kahden kuvan sarjan ja laskea nopeuden tietämällä luodin kahden sijainnin välisen eron ja sen kahden esiintymisen välisen ajan. Miten tahansa teemme sen, meidän on mitattava massa, sijainti ja esiintymisten välinen aika. Päädymme tekemään vähintään kaksi mittausta, jotta saamme x:n ja p:n. Tällöin meidän on valittava, mikä mittaus tehdään ensin ja mikä sitten. Näyttää siltä, että sillä ei ole merkitystä, missä järjestyksessä mittaukset tehdään. Mittaamalla luodin massa ja mittaamalla sitten sen sijainnit kahdesti tai mittaamalla luodin sijainnit kahdesti ja ottamalla sitten luoti takaisin ja mittaamalla sen massa ei olisi mitään eroa, eihän? Loppujen lopuksi emme ole tehneet luodille mitään, kun punnitsemme sen tai kun otamme siitä valokuvia.

Hyvin pienessä mittakaavassa, kun mittaamme jotain elektronin kaltaista, jokainen mittaus tekee sille kuitenkin jotakin. Jos mittaamme ensin sijainnin, muutamme samalla sen momenttia. Jos mittaamme ensin elektronin momentin, muutamme samalla sen sijaintia. Toivomme, että voisimme mitata ensin toisen ja sitten toisen, ennen kuin mikään muuttuu, mutta mittaaminen itsessään aiheuttaa muutoksen, ja paras, mitä voimme toivoa tekevämme, on vähentää mahdollisimman pieneksi sen energian, jonka annamme elektronille mittaamalla sitä. Tuon energian vähimmäismäärän yhtenä tekijänä on Planckin vakio.

Epävarmuus ylittää matriisimatematiikan

Heisenbergin epävarmuusperiaate löytyi "uuden" kvanttifysiikan varhaisimmista yhtälöistä, ja teoria annettiin matriisimatematiikan avulla. Epävarmuusperiaate on kuitenkin tosiasia luonnosta, ja se näkyy myös muissa tavoissa puhua kvanttifysiikasta, kuten Erwin Schrödingerin tekemissä yhtälöissä.

Luonnon määrittelemättömyys, ei ihmisten epävarmuus.

Heisenbergin havaintoja on tarkasteltu kahdella hyvin erilaisella tavalla: Toisin sanoen asiat tapahtuvat tietyn säännön mukaan, ja jos tietäisimme kaiken tarvittavan, voisimme aina sanoa, mitä seuraavaksi tapahtuu. Toiset ajattelevat, että luonnossa tapahtuvia asioita ohjaa vain todennäköisyys, ja voimme tietää vain, miten asiat käyttäytyvät keskimäärin - mutta tiedämme sen hyvin tarkasti.

Fyysikko John Stewart Bell keksi keinon todistaa, että ensimmäinen tapa ei voi olla oikea. Hänen työtään kutsutaan Bellin teoreemaksi tai Bellin epätasa-arvoksi.

Populaarikulttuuri

Ilmaisun "kvanttihyppy" tai "kvanttihyppy" on katsottu tarkoittavan jotakin suurta ja mullistavaa muutosta, ja poliitikot ja joukkotiedotusvälineiden myyntikampanjat käyttävät sitä usein liioitelluissa ilmaisuissa. Kvanttimekaniikassa sitä käytetään kuvaamaan elektronin siirtymistä yhdeltä radalta atomin ytimen ympärillä jollekin toiselle, korkeammalle tai alemmalle radalle.

Joskus sanaa "kvantti" käytetään kaupallisten tuotteiden ja yritysten nimissä. Esimerkiksi Briggs and Stratton valmistaa monenlaisia pieniä bensiinimoottoreita ruohonleikkureihin, maanmuokkaajiin ja muihin vastaaviin pienkoneisiin. Yksi niiden mallinimistä on "Quantum".

Koska epävarmuusperiaate kertoo, että tiettyjä atomitason mittauksia ei voida tehdä häiritsemättä muita mittauksia, jotkut ihmiset käyttävät tätä ajatusta kuvaamaan inhimillisessä maailmassa esiintyviä tapauksia, joissa tarkkailijan toiminta muuttaa tarkkailtavaa asiaa. Antropologi voi mennä johonkin kaukaiseen paikkaan oppiakseen, miten ihmiset siellä elävät, mutta se, että siellä on vieras henkilö ulkomaailmasta tarkkailemassa heitä, voi muuttaa näiden ihmisten toimintatapoja.

Tarkkailijaefektin tapauksia ovat asiat, joita ihmiset tekevät havainnoidessaan asioita, jotka muuttavat havainnoitavaa. Jotkin ihmisten tekemät asiat aiheuttavat muutoksia hyvin pienellä atomien tasolla, ja ne ovat Heisenbergin ensimmäisenä kuvaaman epävarmuuden tai määrittelemättömyyden tapauksia. Epävarmuusperiaate osoittaa, että on aina olemassa raja sille, kuinka pieniä mittauksia voimme tehdä tietyistä mittauspareista, kuten sijainnista ja nopeudesta tai liikeradasta ja liikemäärästä. Havainnointivaikutus kertoo, että joskus sillä, mitä ihmiset tekevät havainnoidessaan asioita, esimerkiksi oppimalla muurahaispesästä kaivamalla sen esiin puutarhatyökaluilla, voi olla suuria vaikutuksia, jotka muuttavat sitä, mitä he yrittivät oppia.