Kultainen leikkaus

Kun on olemassa luku a ja toinen pienempi luku b, näiden kahden luvun suhde saadaan jakamalla ne. Niiden suhde on a/b. Toinen suhdeluku saadaan laskemalla nämä kaksi lukua yhteen ja jakamalla se suuremmalla luvulla a. Uusi suhdeluku on (a+b)/a. Jos nämä kaksi suhdelukua ovat yhtä suuria kuin sama luku, tätä lukua kutsutaan kultaiseksi suhteeksi. Kreikkalainen kirjain φ \displaystyle \varphi } $\varphi$ (phi) käytetään yleensä kultaisen suhteen nimenä.

Jos esimerkiksi b = 1 ja a/b = φ \displaystyle \varphi } $\varphi$ , niin a = φ {\displaystyle \varphi } $\varphi$ . Toinen suhde (a+b)/a on tällöin ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi }. $(\varphi +1)/\varphi$ . Koska nämä kaksi suhdelukua ovat yhtä suuret, tämä on totta:

φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}} $\varphi ={\frac {\varphi +1}{\varphi }}$

Yksi tapa kirjoittaa tämä luku on

φ = 1 + 5 2 = 1.618... {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618...} $\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618...$

5 {\displaystyle {\sqrt {5}}} ${\sqrt {5}}$ on luku, joka kerrottuna itsellään tekee 5: 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5} . ${\sqrt {5}}\times {\sqrt {5}}=5$

Kultaista leikkausta kutsutaan irrationaaliluvuksi. Se tarkoittaa, että jos sitä yrittää kirjoittaa, se ei koskaan lopu eikä muodosta kaavaa, vaan alkaa näin: 1.6180339887... Tärkeä asia tässä luvussa on se, että jos siitä vähennetään 1 tai sillä jaetaan 1, saadaan sama luku.

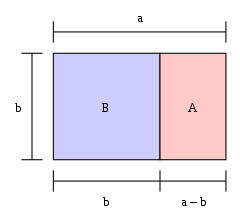
Kultainen suorakulmio

Jos suorakulmion pituus jaettuna sen leveydellä on yhtä suuri kuin kultainen leikkaus, suorakulmio on "kultainen suorakulmio". Jos kultaisen suorakulmion toisesta päästä leikataan neliö, toinen pää on uusi kultainen suorakulmio. Kuvassa iso suorakulmio (sininen ja vaaleanpunainen yhdessä) on kultainen suorakulmio, koska a / b = φ \displaystyle a/b=\varphi } $a/b=\varphi$ . Sininen osa (B) on neliö, ja vaaleanpunainen osa yksinään (A) on toinen kultainen suorakulmio, koska b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi }. $b/(a-b)=\varphi$ . Isolla suorakulmiolla ja vaaleanpunaisella suorakulmiolla on sama muoto, mutta vaaleanpunainen suorakulmio on pienempi ja kääntynyt.

Suuri suorakulmio BA on kultainen suorakulmio, eli suhde b:a on 1: φ \displaystyle \varphi $\varphi$ . Jos mistä tahansa tällaisesta suorakulmiosta, ja vain sellaisista suorakulmioista, joilla on tämä tietty suhde, poistetaan neliö B, jäljelle jää A, joka on toinen kultainen suorakulmio, eli jolla on samat mittasuhteet kuin alkuperäisellä suorakulmiolla.

Fibonaccin luvut

Fibonaccin luvut ovat numeroiden luettelo. Henkilö voi löytää luettelon seuraavan numeron laskemalla yhteen kaksi viimeistä numeroa. Jos henkilö jakaa luettelossa olevan luvun sitä edeltävällä luvulla, suhde lähestyy yhä enemmän kultaista leikkausta.

Fibonaccin luku	jaettuna aiemmalla	suhde
1
1	1/1	= 1.0000
2	2/1	= 2.0000
3	3/2	= 1.5000
5	5/3	= 1.6667
8	8/5	= 1.6000
13	13/8	= 1.6250
21	21/13	= 1.6154...
34	34/21	= 1.6190...
55	55/34	= 1.6177...
89	89/55	= 1.6182...
...	...	...
	φ \displaystyle \varphi } $\varphi$	= 1.6180...

Kultainen leikkaus luonnossa

Luonnossa kultaista leikkausta käytetään usein lehtien tai kukkien asetteluun. Näissä käytetään kultaista kulmaa, joka on noin 137,5 astetta. Tähän kulmaan asetetut lehdet tai kukat hyödyntävät parhaiten auringonvaloa.

Lisäksi henkilön vartalon keskipisteen ja lattian välinen etäisyys sekä pään kruunun ja selkärangan tyven välinen etäisyys ovat molemmat kultaisen leikkauksen mukaisia. Vaikka Leonardo Fibonaccin havainto puuttuu yleisistä arkkitehtuuri- ja suunnittelumalleista, se tunnustetaan laajalti uraauurtavaksi. Se voi esiintyä hurrikaaneissa, norsun syöksyhampaissa, muurahaisissa, merisiileissä, meritähdissä, mehiläisissä ja monissa muissa asioissa.

Fibonacci-sarja alkaa luvulla 0 ja jatkuu ikuisesti: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Ennen jokaista numeroa on kahden numeron summa. Kuvio itsessään on melko alkeellinen ja merkityksetön.

Kunnes opit, että tämä suhde on Mona Lisan kauneuden, ihmisen raajojen, tietojen salauksen ja jopa auringonkukan pään spiraalien lukumäärän taustalla. Näyttää siltä, että maailmankaikkeudella on luonnollinen tapa pitää kirjaa numeroista.

Kukissa on aina pariton määrä terälehtiä, jotka noudattavat Fibonaccin järjestystä. Esimerkiksi rauhanliljalla on kolme terälehteä, päivänkakkaralla viisi, sikurilla 21, päivänkakkaralla 34 ja niin edelleen.

Seuraavassa on muutamia kultaisen leikkauksen luonnollisia esiintymiä:

Siemenpäät. Kukat tuottavat siemeniä ytimestään, jotka sitten kiertyvät ulospäin ja täyttävät kukan pään.

Ananaksia, kukkakaaleja ja roomalaisparsakaalia. Nämä ovat myös Fibonaccin järjestyksen mukaisia.

Käpyjä. Käpyjen siemenkodissa on spiraalikuvio, jossa kussakin käpyyn on kaksi spiraalia, jotka kasvavat vastakkaisiin suuntiin käpyjen kasvaessa.

Puun oksat. Luonnossa tämä kuvio näkyy, kun puu kehittää oksan ja jakautuu sitten kahteen uuteen kasvupisteeseen. Tällöin vain toinen kahdesta uudesta varresta kasvaa aktiivisesti, kun taas toinen on lepotilassa.

Lintujen lentomenetelmät. Haukan paras hyökkäyskulma on kohtisuorassa kohteen lentorataan nähden, mikä on sama kuin spiraalin nousukulma.

Kierregalaksit. Linnunradassa on useita spiraalihaaroja, joista jokaisen logaritminen spiraali on noin 12 astetta.

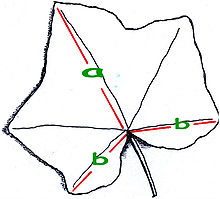
Muratti, jossa näkyy kultainen leikkaus

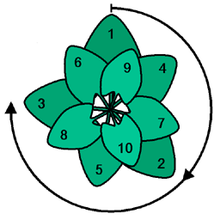
Käyttämällä kultaista kulmaa voit hyödyntää auringon valon optimaalisesti. Tämä on näkymä ylhäältä.

Aiheeseen liittyvät sivut

Fibonaccin luvut
Phi

Kysymyksiä ja vastauksia

K: Mikä on kahden luvun suhde?

V: Kahden luvun suhde saadaan jakamalla ne, joten suhde olisi a/b.

K: Miten toinen suhdeluku voidaan löytää?

V: Toinen suhdeluku voidaan löytää laskemalla kaksi lukua yhteen ja jakamalla tämä summa suuremmalla luvulla a. Tämä uusi suhdeluku olisi (a+b)/a.

K: Mikä on nimitys sille, kun nämä kaksi suhdelukua ovat yhtä suuret?

V: Kun nämä kaksi suhdelukua ovat yhtä suuret, sitä kutsutaan kultaiseksi leikkaukseksi. Se esitetään yleensä kreikkalaisella kirjaimella צ tai phi.

K: Jos b = 1 ja a/b = צ , mitä se tarkoittaa a:lle?

V: Jos b = 1 ja a/b = צ , se tarkoittaa, että myös a = צ.

K: Miten tämä luku voidaan kirjoittaa?

V: Yksi tapa kirjoittaa tämä luku on צ = 1 + 5 / 2 = 1,618....

K: Mitä tarkoittaa, jos siitä vähennetään 1 tai sillä jaetaan 1?

V: Jos siitä vähennetään 1 tai sillä jaetaan 1, saadaan takaisin sama luku - toisin sanoen molemmat vastaavat kultaista leikkausta.

K: Onko kultainen suhde irrationaalinen luku?

V: Kyllä, kultainen suhdeluku on irrationaalinen luku, mikä tarkoittaa, että jos joku yrittää kirjoittaa sen ylös, loppua ei tule koskaan eikä mitään kaavaa - vain alku on jotain tyyliin "1,6180339887...".