Lineaarinen funktio

Perusmatematiikassa lineaarinen funktio on funktio, jonka kuvaaja on suora viiva 2-ulotteisessa avaruudessa (katso kuvat). Esimerkki on: y=2x-1. Korkeammassa matematiikassa lineaarisella funktiolla tarkoitetaan usein lineaarista kartoitusta.

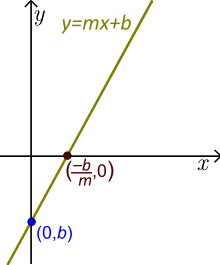
Lineaarinen funktio (Viiva on tässä yleinen. Se on vino, joten m≠0. Katso esimerkit, joissa m:n ja b:n todelliset arvot ovat alla).

Perusominaisuudet

Muodollisesti lineaarinen funktio on sellainen funktio f(x):R→R, että f:n kuvaaja on suora. Tämä tarkoittaa, että f:n alue eli tuloalue on reaaliluku R ja f:n alue eli lähtöalue on myös reaaliluku R. Yleensä f(x):n sijasta kirjoitetaan y(x) tai vain y. Muodollinen lauseke tarkoittaa siis:

syötämme tai korvaamme reaaliluvun x lineaariseen funktioon
lineaarinen funktio tuottaa tai antaa reaaliluvun y ja
kaikki nämä pisteet (x,y) muodostavat viivan.

Lineaarisia funktioita voidaan kirjoittaa kolmessa eri muodossa: kaltevuus, vakio ja parametrinen.

Kaltevuuden leikkauspisteen muoto

Lineaarisen funktion kaltevuus- ja leikkauskulma (jota kutsutaan myös piste-kaltevuudeksi tai eksplisiittiseksi muodoksi) on y ( x ) = m x + b {\displaystyle y(x)=mx+b} $y(x)=mx+b$ tai y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Tässä muodossa on 2 muuttujaa x ja у sekä 2 vakiota m ja b.

Kirjaimet m ja b ovat vakioita. Ennen kuin työskentelemme lineaarisen funktion kanssa, korvaamme m:n ja b:n todellisilla reaaliluvuilla.
Kirjaimet x ja y ovat muuttujia.

Muuttujaa x kutsutaan riippumattomaksi muuttujaksi tai argumentiksi. Mikä tahansa reaaliluku x voidaan syöttää tai korvata lineaarifunktioon. Tämän jälkeen funktio antaa tulokseksi vastaavan arvon y:lle.
Muuttujaa y kutsutaan riippuvaiseksi muuttujaksi. Se on lähtöarvo sen jälkeen, kun x on korvattu tuloarvolla.

Vaakaviivat ovat mukana. Suora on vaakasuora, jos ja vain jos m=0. Silloin on vain y=b. Koska b on reaaliluku, kyseessä on vakiofunktio. Vakiofunktio on siis myös lineaarinen funktio.
Pystyviivoja ei koskaan oteta mukaan, koska pystyviiva ei ole funktio. Pystyviiva ei läpäise pystyviivatestiä. (Pystysuora määritellään yhtälöllä x=b, jossa b on reaaliluku.)
Vinot viivat ovat mukana. Viiva on vino, jos ja vain jos m≠0.

Kaltevuuden leikkauspisteen muoto on ainutlaatuinen. Eri m:n arvo tai eri b:n arvo antaa eri suoran.
Lineaarinen funktio on ensimmäisen tai nolla-asteen polynomifunktio yhdessä muuttujassa х .
Vakiotermi on b. Jos korvataan funktio x=0, saadaan y=b. Luku b on siis y-katkoviiva ja suora leikkaa у-akselin pisteessä (0,b).
Jos m≠0, luku^–b /_m on x-välin leikkauspiste tai juuri tai nolla ja (^–b /_m ,0) on piste, jossa suora ylittää х-akselin. Tässä funktion arvo on nolla.
Kertoimen x kerrointa m kutsutaan suoran kaltevuudeksi tai kaltevuudeksi. Jokaisella suoralla luku m on vakio, joten kaltevuus on vakio koko suoralla. Kaltevuus määrittää sekä suoran suunnan että jyrkkyyden. Suuntaa ja jyrkkyyttä kutsutaan muutosnopeudeksi. Muutosnopeus on siis m ja se on vakio jokaiselle suoralle.

Suunnan määrää m:n merkki. Jos m>0, lineaarinen funktio on kasvava; jos m<0, funktio on laskeva.
Jyrkkyys määräytyy m:n absoluuttisen arvon perusteella. Jos |m|<1, kaltevuus on loiva; jos |m|>1, kaltevuus on jyrkkä.
Jos suoran kaltevuus on m ja (х,у) on jokin piste suoralla, myös piste (х+1, y+m) on oltava suoralla.

Esimerkki: y=-2x+4. Kaltevuus on m= -2 ja y-piste on b=4 eli piste (0,4). Korvaamalla y=0 ja ratkaisemalla x:n suhteen saadaan 0=-2x+4 tai x=2. Eli x=2 on tämän lineaarisen funktion juuri ja piste (2,0) on x-piste. Koska kaltevuus on m = -2, suora on laskeva. Koska |-2|=2>1, lasku on suhteellisen jyrkkä. Jokaisella х:n muutoksella 1 (oikealle) у:n arvo muuttuu -2 (laskee).

Viivan kuvaaja määräytyy kahden pisteen perusteella. Lineaarisen funktion kuvaajaa varten voimme korvata funktion kahdella eri x-arvolla ja ratkaista vastaavat y-arvot. Kuvaamme nämä kaksi pistettä graafisesti. Piirretään viivoitinta käyttäen näiden kahden pisteen läpi viiva, joka jatkuu molempien pisteiden ohi.

Esimerkki: y=-2x+4. Korvaamalla x=0 saadaan y=4 (tämä on y-pisteen leikkauspiste) ja siten piste (0,4). Korvaamalla x=1 saadaan y=2 ja siten piste (1,2). Piirrä nämä pisteet ja piirrä suora. (Huomaa, että 2. piste on 1 pisteen oikealla puolella ja 2 pisteen alapuolella 1. pisteestä). Kuten sanoimme edellä olevassa esimerkissä, tämä johtuu siitä, että kaltevuus on m= -2.)

Lineaarinen funktio, joka ei ole vakiofunktio, on bijektio. Se tuottaa jokaisen reaaliluvun (surjektio) täsmälleen yhdelle tuloarvolle (injektio).

Esimerkki: y= -x+2. Oletetaan, että y= -1. Korvataan y= -1 ja saadaan: -1= -'x+2 tai x=3. Tämä on ainoa ratkaisu. Tämä voidaan tehdä mille tahansa y-arvolle.

Vakiolomake

A x + B y = C , B ≠ 0 {\displaystyle Ax+By=C,\,B\neq 0} $Ax+By=C,\,B\neq 0$ .

Vakiomuodossa on kaksi muuttujaa x ja у sekä kolme vakiota A, B ja C, jotka korvataan todellisilla reaaliluvuilla ennen työskentelyä. Tätä muotoa käytetään usein geometriassa ja lineaaristen yhtälöiden järjestelmissä.

Esimerkki: Lineaarinen funktio 3x-2y=1 on vakiomuodossa. Vakiot ovat A=3, B=-2 ja C=1.

Tämä muoto kirjoitetaan joskus seuraavasti: A x + B y + C = 0 {\displaystyle Ax+By+C=0} $Ax+By+C=0$ . Sen sijaan, että kirjoitetaan 3x-2y=1, kirjoitetaan vastaava yhtälö 3x-2y-1=0.
Vakiot A, B ja C eivät ole yksiselitteisesti määritettävissä. Jos ne kerrotaan kertoimella k, vakioiden arvo muuttuu, mutta viiva on edelleen sama.

Esimerkki: Suorat 3x-2y=1 ja 6x-4y=2 ovat yhtenevät (sama suora). Tässä tapauksessa tekijä on: k=2. Kerroimme ensimmäisen yhtälön luvulla 2 saadaksemme toisen yhtälön. Tämän suoran yksikäsitteinen kaltevuuden leikkauspisteen muoto on: y=1,5x-0,5 (ratkaise jompikumpi yhtälö y:lle).

Vektoriparametrinen muoto

Parametrinen muoto: { x ( t ) = x 1 + a 1 t y ( t ) = y 1 + a 2 t a 1 ≠ 0 , t ∈ R {\displaystyle \left\{\begin{array}{*{20}{l}}}{x(t)={x_{1}}}+{a_{1}}}t}\\\\{y(t)={y_{1}}+{a_{2}}t}\end{array}}\right.\,{a_{1}\neq 0}\,,\,t\in \mathbb {R} } $\left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}+{a_{1}}t}\\{y(t)={y_{1}}+{a_{2}}t}\end{array}}\right.\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ tai

Vektorimuoto: X = ( x 1 , y 1 ) + t ( a 1 , a 2 ) {\displaystyle {\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}}},{a_{2}})} ${\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}},{a_{2}})$ tai r ( t ) = < x 1 + a 1 t , y 1 + a 2 t > , a 1 ≠ 0 , t ∈ R {\displaystyle r(t)=\,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>\,\,\,{a_{1}\neq 0}\,\,\,t\in \mathbb {R} } $r(t)=\,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>\,,\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ .

Parametrisessa tai vektori- tai vektori-parametrisessa muodossa on 1 parametri t, 2 muuttujaa x ja у ja 4 vakiota a₁ , a₂ , x₁ ja y₁ . Kertoimet a₁ , a₂ , x₁ ja y₁ eivät ole yksikäsitteisesti määritettyjä. Suora kulkee pisteiden А=(x₁ ,y₁ ) ja B=(x₁ +a₁ ,y₁ +a₂ ) kautta, joten jos otetaan jokin muu piste tai jopa vain käännetään pisteiden järjestys, saadaan samalle suoralle eri vakiot.
Parametri t ei näy kuvaajassa.
Insinöörit käyttävät parametrista yleensä kirjainta t. Matemaatikot käyttävät usein kreikkalaista kirjainta λ.

Esimerkki: X=(-1,1)+t(2,3), t∈R on vektorimuotoinen viiva. Tässä: a₁ =2, a₂ =3, x₁ =-1 ja x₂ =1. Suora kulkee pisteiden (x₁ ,y₁ )=(-1,1) ja (x₁ +a₁ ,y₁ +a₂ )=(1,4) kautta. Tätä suoraa vastaava parametrimuoto on: x(t)= -1+2t, y(t)=1+3t. Tämän suoran yksikäsitteinen kaltevuuden leikkauspisteen muoto on: y(x)=1,5x+2,5 (ratkaise ensimmäinen yhtälö t:n suhteen ja korvaa tämä tulos toiseen yhtälöön).

Viivan vektoriparametrinen muoto ulottuu luonnollisesti myös 3-ulotteisten ja sitä suurempien tilojen viivoihin. Muut muodot eivät sovellu.

Esimerkki: X=(-1,1,2)+t(2,3,-1), t∈R on viiva 3-ulotteisessa avaruudessa. Suora kulkee pisteiden (-1,1,2) ja (1,4,1) kautta.

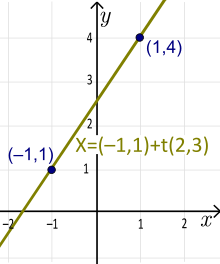
Viivan vektoriparametrinen muoto (ei-yksikäsitteinen). Yksilöllinen kaltevuuden leikkauspisteen muoto on y=1,5x+2,5.

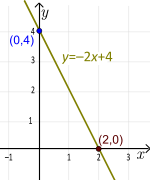
Suoran kaltevuuden ja leikkauspisteen muoto (ainutlaatuinen)

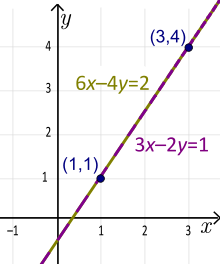
Viivan vakiomuoto (ei-yksilöllinen). Yksilöllinen kaltevuuden leikkauspisteen muoto on y=1,5x-0,5.

Lineaarisen funktion derivaatta

Siinä yhteydessä, jossa se on määritelty, funktion derivaatta on mitta, joka kuvaa funktion arvojen muutosnopeutta suhteessa tuloarvojen muutokseen. Lineaarisen funktion muutosnopeus on vakio. Tämä muutosnopeus on kaltevuus m. Joten m on derivaatta. Tämä kirjoitetaan usein seuraavasti:

( m x + b ) ′ = m {\displaystyle (mx+b)^{\prime }=m} $(mx+b)^{\prime }=m$

Esimerkki: y= -2x+4. Tässä m= -2, joten y′= -2.

Lineaarinen funktio vs. Lineaarinen yhtälö

Usein termit lineaarinen yhtälö ja lineaarinen funktio sekoitetaan keskenään. Molemmat ovat polynomeja. Lineaarisen yhtälön sana lineaarinen tarkoittaa kuitenkin sitä, että kaikki muuttujatermit ovat ensimmäisen asteen termejä. (Lineaarisen funktion sana lineaarinen tarkoittaa, että kuvaaja on viiva.) Lineaarisessa yhtälössä voi olla 1, 2, 3 tai useampia muuttujia. Lineaarinen yhtälö on siis lineaarinen funktio vain, jos siinä on täsmälleen 2 muuttujaa. (Yhden muuttujan lineaarinen yhtälö on piste numeroviivalla ja kolmen muuttujan lineaarinen yhtälö on taso kolmiulotteisessa avaruudessa).

Merkintä

Monet maat ja tieteenalat käyttävät eri kirjaimia ja järjestystä eri muodoista.

Monissa maissa lineaarinen funktio kirjoitetaan usein muodossa y = a x + b {\displaystyle y=ax+b} $y=ax+b$ jossa a on kaltevuus ja b on y-katkoviiva.

Liiketaloudessa ja taloustieteessä lineaarinen funktio kirjoitetaan usein muodossa y = a + b x {\displaystyle y=a+bx} $y=a+bx$ jossa a on y:n leikkauspiste ja b on kaltevuus.

Aiheeseen liittyvät sivut

Linja
Polynomi
Vakiotoiminto
Kvartaalinen yhtälö
Lineaarinen yhtälö