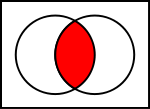
Venn-kaavio (Venn-diagrammi) — joukkojen looginen suhde visualisoituna
Venn-kaavio (Venn-diagrammi) — selkeä visuaalinen opas joukkojen loogisiin suhteisiin: historia, periaatteet ja käytännön esimerkit logiikasta, tilastoista ja tietojenkäsittelystä.
Venn-kaavio on kaavio, joka osoittaa joukkojen välisen loogisen suhteen. John Venn teki ne tunnetuksi 1880-luvulla, ja niitä käytetään nykyään laajalti. Niitä käytetään joukkojen teorian alkeisopetuksessa ja havainnollistamaan yksinkertaisia joukkojen välisiä suhteita todennäköisyydessä, logiikassa, tilastotieteessä, kielitieteessä ja tietojenkäsittelytieteessä. Venn-diagrammissa käytetään tasoon piirrettyjä suljettuja käyriä kuvaamaan joukkoja. Hyvin usein nämä käyrät ovat ympyröitä tai ellipsejä.
Peruskäsitteet ja merkintä
Venn-kaaviolla esitetään joukkojen välisiä perusoperaatioita visuaalisesti. Tavallisia käsitteitä ovat:
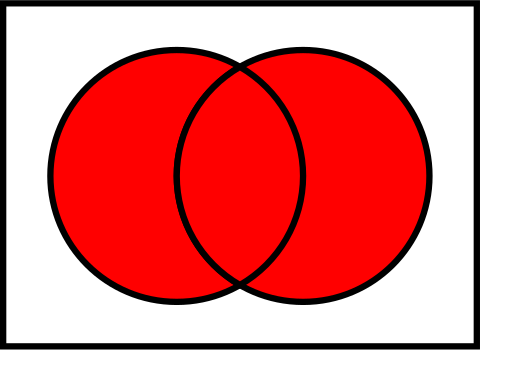
- Yhdiste (A ∪ B): kaikki elementit, jotka kuuluvat vähintään toiseen joukkoon.
- Leikkaus (A ∩ B): ne elementit, jotka kuuluvat molempiin joukkoihin.
- Erotus (A \ B): ne elementit, jotka ovat A:ssa mutta eivät B:ssä.
- Komplementti (A^c): ne elementit, jotka eivät kuulu joukkoon A, yleensä suhteessa jonkin universumin U.
- Tyhjä joukko: kaaviossa alue, johon ei liity yhtään elementtiä.
Esimerkiksi kahden joukon kaaviossa kaksi ympyrää leikkaavat: leikkaus on niiden päällekkäinen alue ja yhdiste koko niiden yhteispinta-ala. Kolmen joukon kaaviossa on yleensä 8 erillistä aluetta (2^3), koska jokaisella elementillä voi olla jokaisesta kolmesta joukosta joko kuuluminen tai kuulumattomuus.
Esimerkkisääntöjä
- P(A ∪ B) = P(A) + P(B) − P(A ∩ B) (todennäköisyyksissä käytetty yleinen yhtälö).
- A \ B = A ∩ B^c (ero voidaan ilmaista leikkauksen ja komplementin avulla).
- Symmetrinen erotus A Δ B on alue, joka kuuluu kummankin joukkoon vuorotellen mutta ei niiden leikkaukseen (eli (A \ B) ∪ (B \ A)).
Variaatiot ja rajoitukset
Perinteiset Venn-kaaviot eivät ota huomioon aluetoimien pinta-alojen tai mittasuhteiden oikeaa suhdetta — ne kuvaavat loogisia suhteita, eivät välttämättä määrällisiä osuuksia. Jos halutaan esittää joukkojen suhteiden kokoja tarkasti, käytetään alueproportional eli pinta-alaan perustuvia kaavioita tai erityisiä ohjelmistoja.
Venn-kaavioita voi piirtää useammalle kuin kolmelle joukolle, mutta monimutkaisuus kasvaa nopeasti. Erityisesti neljän tai useamman joukon selkeä esitys vaatii usein muita muotoja kuin yksinkertaisia ympyröitä. On olemassa myös niin sanottuja symmetrisiä Venn-diagrammeja ja monimutkaisempia käyrämuotoja, jotka kattavat kaikki 2^n aluetta tietyille n:n arvoille.
Erot Eulerin kaavioihin
Venn-kaavioiden ja Leonhard Eulerin kehittämien Eulerin kaavioiden välillä on tärkeä ero: Venn-kaaviot esittävät kaikki mahdolliset loogiset alueet (kaikki 2^n tapaa), vaikka jokin alue olisikin tyhjä, kun taas Eulerin kaaviot vain näyttävät ne suhteet, jotka todella esiintyvät aineistossa (tyhjät alueet jätetään pois). Tämän takia Eulerin kaaviot voivat olla selkeämpiä tilanteissa, joissa joukkojen väliset suhteet eivät muodosta kaikkia mahdollisia yhdistelmiä.
Historia
Vastaavia ajatuksia oli esitetty jo ennen Venniä. Esimerkiksi Christian Weise vuonna 1712 (Nucleus Logicoe Wiesianoe) ja Leonhard Euler vuonna 1768 (Kirjeitä saksalaiselle prinsessalle) esittivät samanlaisia ajatuksia. John Venn popularisoi ajatuksen teoksessaan Symbolic Logic, luku V "Diagrammatic Representation", 1881. Vennin versio teki erityisesti kolmialaisista ja kahdenlaisista kaavioista laajalti tunnettuja ja opetuksessa yleiskäyttöisiä.
Käyttökohteita
- Todennäköisyyslaskenta: tapahtumien yhteydet ja yhtenäisyyssäännöt.
- Logiikka ja argumentaatio: väitteiden ja predikaattien suhteiden havainnollistaminen.
- Tilastotiede: ryhmien päällekkäisyyksien visualisointi, esimerkiksi riskitekijöiden yhteisvaikutukset.
- Kielitiede: luokkien ja kategorioiden päällekkäisyyksien kuvaus.
- Tietojenkäsittely: tietokantakyselyt, joukko-operaatiot ja hakualgoritmit hyödyntävät samoja periaatteita.
- Biologia ja genetiikka: lajien tai geenien esiintymisen päällekkäisyyksien esitys.
Vaikka Venn-kaaviot ovat yksinkertaisia ja opettavaisia, niitä kannattaa käyttää tarkoituksenmukaisesti: monimutkaisissa tai numeerisesti herkissä tilanteissa tarvitaan usein tarkempia graafisia tai matemaattisia keinoja suhteiden kvantifioimiseksi.
Venn-diagrammit ovat edelleen tehokas työkalu intuitiiviseen ajatteluun ja opetukseen, koska ne muuttavat abstraktin joukko-opin visuaalisesti hahmotettavaksi kuvaksi.

Lasimaalauksia Cambridgessa, jossa John Venn opiskeli. Siinä on Vennin kaavio.
Esimerkki
Seuraavassa esimerkissä käytetään kahta joukkoa, A ja B, jotka esitetään tässä värillisinä ympyröinä. Oranssi ympyrä, joukko A, edustaa kaikkia kaksijalkaisia eläviä olentoja. Sininen ympyrä, joukko B, edustaa eläviä olentoja, jotka voivat lentää. Kukin erillinen oliotyyppi voidaan kuvitella pisteeksi jossakin kohtaa kaaviota. Elävät olennot, jotka voivat sekä lentää että olla kaksijalkaisia - esimerkiksi papukaijat - ovat siis molemmissa joukoissa ja vastaavat siten pisteitä alueella, jossa sininen ja oranssi ympyrä ovat päällekkäin. Tämä alue sisältää kaikki (ja vain) tällaiset elävät olennot.
Ihmiset ja pingviinit ovat kaksijalkaisia, joten ne ovat oranssissa ympyrässä, mutta koska ne eivät osaa lentää, ne ovat oranssin ympyrän vasemmassa osassa, jossa se ei ole päällekkäin sinisen ympyrän kanssa. Hyttysillä on kuusi jalkaa, ja ne lentävät, joten hyttysten piste on sinisen ympyrän siinä osassa, joka ei ole päällekkäinen oranssin ympyrän kanssa. Oliot, jotka eivät ole kaksijalkaisia eivätkä osaa lentää (esimerkiksi valaat ja hämähäkit), edustaisivat kaikki pisteitä molempien ympyröiden ulkopuolella.
Joukkojen A ja B yhdistettyä aluetta kutsutaan joukkojen A ja B liitoksi, jota merkitään A ∪ B. Tässä tapauksessa liitossa ovat mukana kaikki elävät olennot, jotka ovat joko kaksijalkaisia tai jotka voivat lentää (tai molemmat). Sekä A:ssa että B:ssä olevaa aluetta, jossa nämä kaksi joukkoa ovat päällekkäin, kutsutaan A:n ja B:n leikkauspisteeksi, jota merkitään A ∩ B. Esimerkiksi näiden kahden joukon leikkauspiste ei ole tyhjä, koska siinä on pisteitä, jotka edustavat sekä oranssiin että siniseen ympyrään kuuluvia olioita.
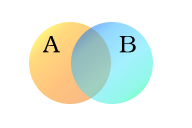
Sarjat A (kaksijalkaiset olennot) ja B (lentävät olennot).
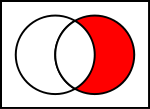
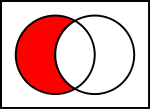
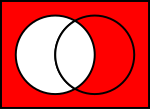
Joukkojen yleisten operaatioiden Venn-diagrammit
Alla olevissa kuvissa vasen ympyrä osoittaa joukkoa 

Aiheeseen liittyvät sivut
- Yksinomainen disjunktio
- Inklusiivinen disjunktio
Kysymyksiä ja vastauksia
K: Mikä on Venn-diagrammi?
A: Venn-diagrammi on kaavio, joka osoittaa joukkojen välisen loogisen suhteen. Siinä käytetään tasoon piirrettyjä suljettuja käyriä, yleensä ympyröitä tai ellipsejä, kuvaamaan joukkoja.
K: Kuka teki Venn-diagrammit tunnetuksi?
V: John Venn teki Venn-diagrammit tunnetuksi 1880-luvulla.
K: Mihin niitä käytetään?
V: Niitä käytetään joukkojen teorian alkeiden opettamiseen ja yksinkertaisten joukkojen suhteiden havainnollistamiseen todennäköisyydessä, logiikassa, tilastotieteessä, kielitieteessä ja tietojenkäsittelytieteessä.
K: Kuka esitti vastaavia ajatuksia ennen John Venniä?
V: Christian Weise ehdotti samankaltaisia ajatuksia vuonna 1712 teoksessaan Nucleus Logicoe Wiesianoe ja Leonhard Euler ehdotti niitä kirjassaan Letters to a German Princess vuonna 1768.
K: Milloin John Venn julkaisi Symbolisen logiikan?
V: John Venn julkaisi Symbolic Logic -kirjan vuonna 1881.
Kysymys: Missä Symbolic Logic -teoksen luvussa John Venn popularisoi Venn-diagrammin idean?
V: John Venn teki Venn-diagrammin idean tunnetuksi Symbolista logiikkaa käsittelevässä luvussa 5 "Diagrammatinen esittäminen".
K: Miten nämä ajatukset esitettiin ennen Venn-diagrammin nykyaikaisen version keksimistä?
V: Ennen V enn-diagrammin nykyaikaisen version keksimistä nämä ajatukset esitettiin käyttämällä tasoon piirrettyjä suljettuja käyriä, kuten ympyröitä tai ellipsejä.
Etsiä