Harmoninen sarja

Matematiikassa harmoninen sarja on divergentti ääretön sarja:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergentti tarkoittaa, että kun lisäät lisää termejä, summa ei koskaan lakkaa kasvamasta. Se ei mene kohti yhtä äärellistä arvoa.

Ääretön tarkoittaa, että voit aina lisätä uuden termin. Sarjalla ei ole lopullista termiä.

Sen nimi tulee musiikin harmonisista sävelistä: värähtelevän jousen yläsävelten aallonpituudet ovat 1/2,

1/3, 1/4 jne. jousen perusaallonpituudesta. Ensimmäistä termiä lukuun ottamatta sarjan jokainen termi on sen molemmin puolin olevien termien harmoninen keskiarvo. Ilmaisu harmoninen keskiarvo tulee myös musiikista.

Historia

Nicole Oresme todisti 1300-luvulla, että harmoninen sarja divergoi, mutta se unohtui. Pietro Mengoli, Johann Bernoulli ja Jacob Bernoulli toimittivat todistukset 1600-luvulla.

Arkkitehdit ovat käyttäneet harmonisia sekvenssejä. Barokin aikana arkkitehdit käyttivät niitä pohjapiirustusten ja julkisivujen mittasuhteissa sekä kirkkojen ja palatsien arkkitehtonisten yksityiskohtien välisissä suhteissa.

Divergenssi

Harmonisen sarjan divergenssistä on useita tunnettuja todistuksia. Seuraavassa esitetään muutamia niistä.

Vertailutesti

Yksi tapa todistaa divergenssi on verrata harmonista sarjaa toiseen divergenssisarjaan, jossa jokainen nimittäjä korvataan seuraavaksi suurimmalla kahden potenssilla:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}}+{\frac {1}{8}}}+{\frac {1}{9}}+\cdots \\\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+ \cdots \end{aligned}}}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Jokainen harmonisen sarjan termi on suurempi tai yhtä suuri kuin toisen sarjan vastaava termi, joten harmonisen sarjan summan on oltava suurempi tai yhtä suuri kuin toisen sarjan summa. Toisen sarjan summa on kuitenkin ääretön:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Tästä seuraa (vertailutestin avulla), että myös harmonisten sarjojen summan on oltava ääretön. Tarkemmin sanottuna yllä oleva vertailu osoittaa, että

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

jokaiselle positiiviselle kokonaisluvulle $k$ .

Tätä Nicole Oresmen noin vuonna 1350 esittämää todistusta pidetään keskiaikaisen matematiikan huippukohtana. Se on edelleen vakiotodistus, jota opetetaan matematiikan tunneilla nykyäänkin.

Kokonaisvaltainen testi

On mahdollista todistaa, että harmoninen sarja divergoi vertaamalla sen summaa epäsuotuisaan integraaliin. Tarkastellaan oikealla olevassa kuvassa esitettyä suorakulmioiden järjestelyä. Kukin suorakulmio on 1 yksikön levyinen ja

1/n yksikköä korkea, joten äärettömän määrän suorakulmioita kokonaispinta-ala on harmonisten sarjojen summa:

suorakulmioiden pinta-ala = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}\\\{\text{rectangles}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Käyrän alapuolella oleva kokonaispinta-ala $y =$

1/x arvosta 1 äärettömään saadaan divergentti epäsäännöllinen integraali:

käyrän alle jäävä pinta-ala = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}\\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .} ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Koska tämä pinta-ala sisältyy kokonaan suorakulmioihin, myös suorakulmioiden kokonaispinta-alan on oltava ääretön. Tämä todistaa, että

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).} $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Tämän väitteen yleistäminen tunnetaan nimellä integraalitesti.

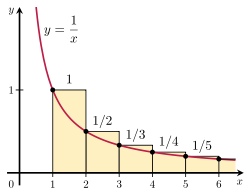
Integraalitestin havainnollistaminen.

Divergenssinopeus

Harmoninen sarja eroaa hyvin hitaasti. Esimerkiksi 10 ensimmäisen⁴³ termin summa on alle 100. Tämä johtuu siitä, että sarjan osasummilla on logaritminen kasvu. Erityisesti,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

jossa $γ$ on Euler-Mascheronin vakio ja $ε k ~$

1/2k, joka lähestyy 0:ta, kun $k$ on ääretön. Leonhard Euler todisti sekä tämän että sen, että summa, joka sisältää vain alkulukujen vastavuoroiset luvut, myös divergoi, toisin sanoen:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}}+{\frac {1}{7}}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .} $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Osasummat

Kolmekymmentä ensimmäistä harmonista lukua
$n$	Harmonisen sarjan osasumma, $H n$
$n$	murtolukuna ilmaistuna		desimaali	suhteellinen koko
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Eroavien harmonisten sarjojen äärelliset osasummat,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

kutsutaan harmonisiksi luvuiksi.

$H n$ ja $ln n:n$ erotus konvergoi Euler-Mascheroni-vakioon. Kahden harmonisen luvun erotus ei ole koskaan kokonaisluku. Yksikään harmoninen luku ei ole kokonaisluku, paitsi $H 1 = 1$ .

Aiheeseen liittyvät sarjat

Vaihtuva harmoninen sarja

Sarja

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

tunnetaan vaihtuvana harmonisena sarjana. Tämä sarja konvergoituu vaihtuvan sarjan testin avulla. Erityisesti summa on yhtä suuri kuin 2:n luonnollinen logaritmi:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Vaihteleva harmoninen sarja on ehdollisesti konvergentti, mutta ei absoluuttisesti konvergentti: jos sarjan termejä järjestetään systemaattisesti uudelleen, summasta tulee yleensä erilainen ja järjestämisestä riippuen mahdollisesti jopa ääretön.

Vaihtuvan harmonisen sarjan kaava on erikoistapaus Mercator-sarjasta, joka on luonnollisen logaritmin Taylor-sarja.

Vastaava sarja voidaan johtaa arktangentin Taylorin sarjasta:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.} $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Tämä tunnetaan Leibnizin sarjana.

Yleinen harmoninen sarja

Yleinen harmoninen sarja on muotoa

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

jossa $a \neq 0$ ja $b$ ovat reaalilukuja ja

b/a ei ole nolla tai negatiivinen kokonaisluku.

Harmonisten sarjojen raja-arvovertailutestin mukaan kaikki yleiset harmoniset sarjat poikkeavat myös toisistaan.

p-sarja

Harmonisen sarjan yleistys on p-sarja (tai hyperharmoninen sarja), joka on määritelty seuraavasti

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

mille tahansa reaaliluvulle $p$ . Kun $p = 1$ , $p-sarja$ on harmoninen sarja, joka divergoi. Joko integraalitesti tai Cauchyn kondensointitesti osoittaa, että $p-sarja$ konvergoi kaikilla $p > 1$ (jolloin sitä kutsutaan yliharmoniseksi sarjaksi) ja divergoi kaikilla $p \leq 1$ . Jos $p > 1$ , niin $p-sarjan$ summa on $ζ (p)$ eli Riemannin zeta-funktio, joka on arvioitu pisteessä $p.$

Ongelmaa, joka koskee summan $p = 2$ löytämistä, kutsutaan Baselin ongelmaksi; Leonhard Euler osoitti, että se on seuraava.

$π$ ² /6. Summan arvoa $p = 3$ kutsutaan Apéryn vakioksi, koska Roger Apéry osoitti, että se on irrationaaliluku.

ln-sarja

P-sarjaan liittyy ln-sarja, joka on määritelty seuraavasti

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

mille tahansa positiiviselle reaaliluvulle $p$ . Tämä voidaan osoittaa integraalitestillä, että se divergoi, kun $p \leq 1,$ mutta konvergoi, kun $p > 1$ .

φ-sarja

Minkä tahansa kuperan, reaaliarvoisen funktion $φ tapauksessa$ , joka on sellainen, että

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}\right)}{\varphi (u)}}<{\frac {1}{2}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

sarja

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

on konvergentti.

Satunnainen harmoninen sarja

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

jossa $s n$ ovat riippumattomia, identtisesti jakautuneita satunnaismuuttujia, jotka saavat arvot +1 ja -1 yhtä suurella todennäköisyydellä.

1/2, on todennäköisyysteoriassa tunnettu esimerkki satunnaismuuttujien sarjasta, joka konvergoi todennäköisyydellä 1. Tämä konvergenssi on helppo seuraus joko Kolmogorovin kolmen sarjan lauseesta tai siihen läheisesti liittyvästä Kolmogorovin maksimaalisesta epätasa-arvosta. Byron Schmuland Albertan yliopistosta tutki edelleen satunnaisen harmonisen sarjan ominaisuuksia ja osoitti, että konvergenssisarja on satunnaismuuttuja, jolla on joitakin mielenkiintoisia ominaisuuksia. Erityisesti tämän satunnaismuuttujan todennäköisyystiheysfunktio, joka arvioidaan +2:ssa tai -2:ssa, saa arvon 0,12499999999999999999999999999999999999999999999999999999999999999999999999999999999764..., mikä poikkeaa arvosta 1/8 alle 10⁻⁴² . Schmulandin artikkelissa selitetään, miksi tämä todennäköisyys on niin lähellä, mutta ei täsmälleen 1/8. Tämän todennäköisyyden tarkka arvo saadaan äärettömän kosinogeenituotteen integraalilla $C 2$ jaettuna $π:llä.$

Poistunut harmoninen sarja

Varttuneen harmonisen sarjan, jossa kaikki termit, joiden nimittäjässä esiintyy numero 9, on poistettu, voidaan osoittaa konvergoivan, ja sen arvo on pienempi kuin 80. Itse asiassa, kun kaikki termit, jotka sisältävät minkä tahansa numerosarjan (missä tahansa perusluvussa tahansa), poistetaan, sarja konvergoituu.

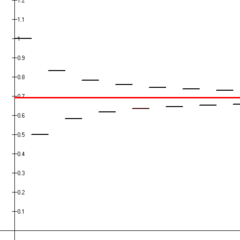
Vuorottelevan harmonisen sarjan neljätoista ensimmäistä osasummaa (mustat viivasegmentit), jotka konvergoituvat 2:n luonnolliseen logaritmiin (punainen viiva).

Sovellukset

Harmoninen sarja voi olla vastakkainen. Tämä johtuu siitä, että se on divergentti sarja, vaikka sarjan termit pienenevät ja menevät kohti nollaa. Harmonisen sarjan divergenssi on joidenkin paradoksien lähde.

"Mato kuminauhan päällä". Oletetaan, että mato ryömii äärettömän elastista yhden metrin pituista kuminauhaa pitkin samaan aikaan, kun kuminauhaa venytetään tasaisesti. Jos mato kulkee yhden senttimetrin minuutissa ja nauha venyy yhden metrin minuutissa, tuleeko mato koskaan kuminauhan päähän? Vastaus on intuitiivisesti "kyllä", sillä $n$ minuutin kuluttua madon kulkeman matkan ja kuminauhan kokonaispituuden suhde on seuraava

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Koska sarja kasvaa mielivaltaisesti, kun $n$ kasvaa, tämän suhteen on lopulta oltava yli 1, mikä tarkoittaa, että mato saavuttaa kuminauhan pään. Sen $n:n$ arvon, jolla tämä tapahtuu, on kuitenkin oltava erittäin suuri: noin e $100$ , luku, joka ylittää 10⁴³ minuuttia (10³⁷ vuotta). Vaikka harmoninen sarja eroaa, se tekee sen hyvin hitaasti.

Jeep-ongelmassa kysytään, kuinka paljon kokonaispolttoainetta tarvitaan, jotta auto, jonka polttoainekapasiteetti on rajallinen, voi ylittää aavikon ja jättää polttoainepisaroita reitin varrelle. Matka, jonka auto voi kulkea tietyllä polttoainemäärällä, liittyy harmonisten sarjojen osasummiin, jotka kasvavat logaritmisesti. Tarvittava polttoainemäärä kasvaa siis eksponentiaalisesti halutun matkan myötä.

Palikoiden pinoamisongelma: Kun on olemassa kokoelma samanlaisia dominopalikoita, on mahdollista pinota ne pöydän reunalle niin, että ne roikkuvat pöydän reunan yli putoamatta. Vastakkainen tulos on, että ne voidaan pinota siten, että ylihangaus on niin suuri kuin halutaan. Siis edellyttäen, että dominopalikoita on tarpeeksi.

Uimari, joka kiihtyy joka kerta, kun hän koskettaa altaan seinää. Uimari aloittaa 10 metrin altaan ylittämisen nopeudella 2 m/s, ja jokaisella ylittämisellä nopeuteen lisätään vielä 2 m/s. Teoriassa uimarin nopeus on rajoittamaton, mutta nopeuden saavuttamiseen tarvitaan hyvin monta altaan ylitystä; esimerkiksi valonnopeuden saavuttamiseksi (ilman erityistä suhteellisuusteoriaa) uimarin on ylitettävä allas 150 miljoonaa kertaa. Vastoin tätä suurta lukua tietyn nopeuden saavuttamiseen tarvittava aika riippuu sarjojen summasta, joka saadaan millä tahansa tietyllä määrällä altaan ylityksiä:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}}\sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Summan laskeminen osoittaa, että valonnopeuden saavuttamiseen tarvitaan vain 97 sekuntia.

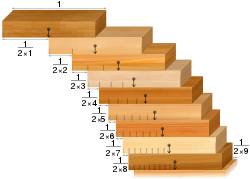
Lohkojen pinoamisongelma: harmonisen sarjan mukaisesti linjatut lohkot ylittävät halkeamia, joiden leveys on mikä tahansa.

Aiheeseen liittyvät sivut

Harmoninen eteneminen
Luettelo vastavuoroisten summista

Kysymyksiä ja vastauksia

Q: Mikä on harmoninen sarja?

V: Harmoninen sarja on ääretön divergenssisarja, jossa jokainen termi on yhtä suuri kuin 1 jaettuna sen sijainnilla sarjassa.

K: Mitä tarkoittaa, että sarja on divergentti?

V: Divergentti tarkoittaa sitä, että kun lisäät lisää termejä, summa ei lakkaa koskaan kasvamasta, eikä mene kohti yhtä äärellistä arvoa.

K: Mitä tarkoittaa, että sarja on ääretön?

V: Ääretön tarkoittaa sitä, että sarjaan voidaan aina lisätä uusi termi ja että sarjassa ei ole lopputermiä.

K: Mistä sarjan nimi on peräisin?

V: Tämän sarjan nimi tulee musiikin harmonisten sävelten ideasta, jossa yläsävelten aallonpituudet ovat 1/2, 1/3, 1/4 jne. jousen perusaallonpituudesta.

K: Mitä harmoninen tarkoittaa?

V: Harmoninen keskiarvo on silloin, kun sarjan jokainen termi on yhtä suuri kuin sen viereisten termien harmoninen keskiarvo. Tämäkin ilmaisu on peräisin musiikista.

K: Miten laskemme tämän jakson jokaisen termin?

V: Jokainen termi tässä sarjassa voidaan laskea jakamalla yksi sen sijainnilla sarjassa (1/n).