Logaritminen spiraali – määritelmä, historia ja esiintyminen luonnossa
Logaritminen spiraali, tasakulmainen spiraali tai kasvuspiraali on erityinen spiraalikäyrä, joka esiintyy usein luonnossa. Logaritmisen spiraalin kuvasi ensimmäisen kerran Descartes, ja myöhemmin sitä tutki laajasti Jakob Bernoulli, joka kutsui sitä Spira mirabilikseksi, "ihmeelliseksi spiraaliksi".
Määritelmä ja perusmuoto
Logaritminen spiraali on tasossa kulkeva käyrä, jonka etäisyys origosta kasvaa eksponentiaalisesti kulman mukaan. Polar-muodossa sen yhtälö on tavallisesti kirjoitettu muodossa
r = a e^{bθ},
missä a ja b ovat reaalisia vakioita ja θ on polarikulma. Tässä r on etäisyys origosta ja e on Neperin luku. Jos b > 0, spiraali kiertyy vastapäivään etääntyen origosta; jos b < 0, se lähestyy originia kierteen kasvaessa.
Tärkeimmät ominaisuudet
- Equiangular (tasakulmainen): logaritmisen spiraalin tärkein ominaisuus on, että se leikkaa aina samaan kulmaan radiaaliviivan (suoran, joka lähtee origosta) kanssa. Tämä kulma on vakio ja riippuu parametrista b. Jos kulma on α, niin b = cot α eli tan α = 1/b.
- Itsesimilaarisuus: skaalaus origon suhteen vastaa rotaatiota. Tarkemmin, kun spiraalia skaalataan kertoimella c > 0, se vastaa spiraalin kiertymistä kulmalla (ln c)/b. Tämä selittää, miksi muoto näyttää samanlaiselta eri mittakaavoissa.
- Analyyttiset esitykset: kartesiassa spiraali voidaan parametrisoida x(θ) = a e^{bθ} cos θ, y(θ) = a e^{bθ} sin θ.
- Kaaren pituus ja pinta-ala: Kaaren pituus välillä θ1..θ2 on s = (a sqrt(1+b^2)/b) [e^{bθ2} − e^{bθ1}]. Kulman välin aiheuttaman sektorin pinta-ala on A = (a^2/(4b)) [e^{2bθ2} − e^{2bθ1}] (olettaen b ≠ 0).
- Kompleksiesitys: spiraali voidaan nähdä eksponenttifunktion kuvana: z(t) = a e^{(b + i) t}, jolloin suora kompleksitasossa muuttuu logaritmiseksi spiraaliksi eksponenttimuunnoksessa.
Historia ja merkitys
Descartes kuvasi spiraalille ominaisia piirteitä 1600-luvulla; myöhemmin 1700-luvulla Jakob Bernoulli tutki sitä perusteellisesti ja ihaili sen kauniita matemaattisia ominaisuuksia. Bernoulli antoi sille lempinimen Spira mirabilis ja toivoi spiraalin kaiverrettavan hautakivelleen yhdessä lauseen kanssa "Eadem mutata resurgo" ("Muututtuani kuitenkin nousen jälleen samana"). Legendan mukaan kiven alkuperäinen koriste oli virheellinen spiraalin sijaan, mutta myöhemmin Bernoullin muistokiveen saatiin oikea spiraali.
Logaritminen spiraali luonnossa ja tekniikassa
Logaritminen spiraali esiintyy monissa luonnollisissa ja ihmisten tekemissä rakenteissa. Esimerkkejä:
- Monet simpukkakodit ja joidenkin murekkeiden kuoret muistuttavat logaritmista spiraalia – huomattava esimerkki on usein mainittu nautilus, vaikka todellinen muoto vaihtelee lajin ja yksilön mukaan.
- Kasvien lehtien ja siemenien asetelmissa esiintyvät spiraalikuvioinnit liittyvät phyllotaksikseen; täsmällinen jakautuma noudattaa usein kultaista kulmaa (~137,5°), mikä tuottaa tiiviin pakkauksen ja johtaa käytännössä lähelle spiraalin kaltaisia muotoja (kuitenkin yksittäiset siemenradat eivät aina ole täsmällisesti logaritmisia).
- Sääilmiöissä ja tähtitieteessä: trooppiset pyörremyrskyt ja monet galaksit näyttävät spiraalimaisilta rakenteilta, jotka paikallisesti voidaan mallintaa logaritmisella spiraalilla.
- Tekniikassa ja arkkitehtuurissa: logaritmista spiraalia hyödynnetään anturisuunnittelussa, tuotemuotoilussa ja estetiikassa, koska muoto säilyttää suhteellisen ulkoasun eri mittakaavoissa.
Erityistapaukset ja yhteydet
- Kultainen spiraali: eräs erikoistapaus on niin kutsuttu kultainen spiraali, joka on logaritminen spiraali, jonka säde kasvaa kultaisen suhdeluvun φ verran jokaisella 90°:n kierroksella. Tämä on matemaattinen erikoistapaus, jota käytetään usein visuaalisen havainnon yhteydessä.
- Erot Archimedeen spiraaliin: Archimedeen spiraalissa etäisyys origosta kasvaa lineaarisesti kulman mukaan (r = a + bθ). Logaritminen spiraali eroaa siten merkittävästi: se kasvaa eksponentiaalisesti eikä ole tasaetäisyyksinen kierrosten välillä.
- Fibonacci ja phyllotaksis: luonnossa esiintyvä siementen ja lehtien jakautuminen liittyy usein Fibonacci-lukuihin ja kultaisen kulman käyttöön. Näiden ilmiöiden geometrinen optimointi johtaa spiraalimaisiin kuvioihin, jotka lähellä logaritmista käyttäytymistä, vaikka tarkka malli voi poiketa ideaalista logaritmisesta spiraalista.
Lisätietoa kaavoista ja laskelmista
Muutama käytännön kaava yhteenvedoksi (r = a e^{bθ}):
- Parametriesitys: x(θ) = a e^{bθ} cos θ, y(θ) = a e^{bθ} sin θ.
- Vakio kulma α radiaaliviivan ja tangentin välillä: tan α = 1/b (siis b = cot α).
- Kaaren pituus θ1 → θ2: s = (a sqrt(1+b^2)/b) [e^{bθ2} − e^{bθ1}].
- Pinta-ala sektorissa θ1 → θ2: A = (a^2/(4b)) [e^{2bθ2} − e^{2bθ1}].
Yhteenveto
Logaritminen spiraali on sekä matematiikan että luonnon kannalta kiinnostava käyrä: sen tasakulmaisuus ja itsesimilarisuus tekevät siitä yleisesti esiintyvän ja helposti tunnistettavan muodon. Se yhdistää yksinkertaisen analyyttisen muodon ja monipuoliset sovellukset luonnontieteissä, muotoilussa ja taiteessa.
Spiraaligalaksien varret ovat usein logaritmisen spiraalin muotoisia, tässä tapauksessa Whirlpool-galaksin.
Islannin yläpuolella oleva matalapainealue on suunnilleen logaritminen spiraalikuvio.
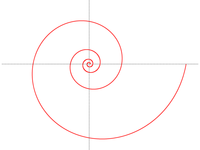
Logaritminen kierre (korkeus 10°)
Nautiluksen kuoren leikkaus, jossa kammiot on järjestetty suunnilleen logaritmiseksi kierteeksi.
Määritelmä
Polaarikoordinaatistossa (r, θ) käyrä voidaan kirjoittaa seuraavasti
r = a e b θ θ \displaystyle r=ae^{b\theta }\,} 
tai
θ = 1 b ln ( r / a ) , {\displaystyle \theta ={\frac {1}{b}}\ln(r/a),} 
tästä nimi "logaritminen". Parametrisessa muodossa käyrä on
x ( t ) = r cos ( t ) = a e b t cos ( t ) {\displaystyle x(t)=r\cos(t)=ae^{bt}\cos(t)\,} 
y ( t ) = r sin ( t ) = a e b t sin ( t ) {\displaystyle y(t)=r\sin(t)=ae^{bt}\sin(t)\,} 
reaaliluvuilla a ja b.
Spiraalilla on se ominaisuus, että tangentin ja säteittäisen suoran välinen kulma ɸ pisteessä (r,θ) on vakio. Tämä ominaisuus voidaan ilmaista differentiaaligeometrisesti seuraavasti
arccos ⟨ r ( θ ) , r ′ ( θ ) ⟩ ‖ r ( θ ) ‖ ‖ ‖ r ′ ( θ ) ‖ = arctan 1 b = ϕ , {\displaystyle \arccos {\frac {\\langle \mathbf {r} (\theta ),\mathbf {r} '(\theta )\rangle }{\|\mathbf {r} (\theta )\|||\|\mathbf {r} '(\theta )\|}}=\arctan {\frac {1}{b}}=\phi ,} 
Derivaatta r'(θ) on verrannollinen parametriin b. Toisin sanoen se säätelee sitä, kuinka "tiukasti" ja mihin suuntaan spiraali kiertyy. Ääritapauksessa b = 0 (ɸ = π/2) spiraali muuttuu ympyräksi, jonka säde on a. Sitä vastoin siinä raja-arvossa, jossa b lähestyy ääretöntä (ɸ → 0), spiraali pyrkii kohti suoraa. ɸ:n komplementtia kutsutaan pituudeksi.
Spira mirabilis ja Jakob Bernoulli
Spira mirabilis, latinaksi "ihmeellinen spiraali", on toinen nimi logaritmiselle spiraalille. Vaikka muut matemaatikot olivat jo nimenneet tämän käyrän, Jakob Bernoulli antoi tälle käyrälle nimen "ihmeellinen" tai "ihmeellinen" spiraali, koska häntä kiehtoi yksi sen ainutlaatuisista matemaattisista ominaisuuksista: spiraalin koko kasvaa, mutta sen muoto pysyy samana jokaisen lisätyn käyrän myötä. Ehkä tämän ominaisuuden vuoksi spira mirabilis on kehittynyt luonnossa, ja sitä on nähty joissakin elävissä olennoissa, kuten nautiluksen kuorissa ja auringonkukan päissä. Jakob Bernoulli halusi tämän muodon hautakiveensä, mutta erehdyksessä sinne sijoitettiin sen sijaan arkimedealainen spiraali.
Logaritmiset spiraalit luonnossa
Useissa luonnonilmiöissä voidaan löytää käyriä, jotka ovat lähellä logaritmisia spiraaleja. Seuraavassa on joitakin esimerkkejä ja syitä:
- Haukan lähestyminen saalistaan. Niiden terävin näkymä on kulmassa niiden lentosuuntaan nähden; tämä kulma on sama kuin spiraalin nousu.
- Hyönteisen lähestyminen valonlähdettä. Ne ovat tottuneet siihen, että valonlähde on vakiokulmassa niiden lentorataan nähden. Tavallisesti aurinko on ainoa valonlähde, ja sen kautta lentäminen johtaa käytännössä suoraan linjaan.
- Spiraaligalaksien varret. Omassa galaksissamme, Linnunradassa, uskotaan olevan neljä suurta spiraalihaaraa, joista kukin on suunnilleen logaritminen spiraali, jonka nousukulma on noin 12 astetta, mikä on Linnunradan kaltaiselle galaksille epätavallisen pieni nousukulma. Yleensä spiraaligalaksien haarojen nousukulmat vaihtelevat noin 10 ja 40 asteen välillä.
- Trooppisten syklonien, kuten hurrikaanien, varret.
|
|
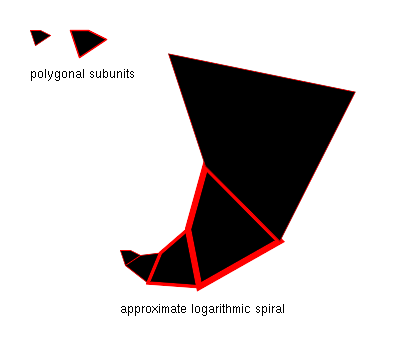
- Monet biologiset rakenteet, kuten hämähäkinseitit ja nilviäisten kuoret. Näissä tapauksissa syy on seuraava: Aloitetaan mistä tahansa epäsäännöllisen muotoisesta kaksiulotteisesta kuviosta F0 . Laajennetaan F0 tietyllä kertoimella, jolloin saadaan F1 , ja asetetaan F1 F0 viereen niin, että kaksi sivua koskettaa toisiaan. Laajennetaan nyt F1 samalla kertoimella, jolloin saadaan F2 , ja sijoitetaan se F1 viereen kuten aiemmin. Toistamalla tätä saadaan likimääräinen logaritminen kierre, jonka korkeus määräytyy laajennuskertoimen ja sen kulman mukaan, jolla luvut asetettiin vierekkäin. Tämä on esitetty monikulmionmuotoisten kuvioiden osalta oheisessa kuvassa.
