Maailmanviiva | ainutkertainen polku, jonka esine kulkee sekä avaruudessa että ajassa
Maailmaviiva on ainutkertainen reitti, jonka kappale kulkee kulkiessaan sekä avaruudessa että ajassa, jota yleensä kutsutaan avaruusajaksi. Kuten opimme erityisestä suhteellisuusteoriasta, mitä nopeammin kappale kulkee, sitä enemmän aika hidastuu kyseisen kappaleen osalta. Kuten oikealla olevasta kuvasta näkyy, hitaamman kappaleen aika kulkee nopeammin kuin hyvin nopean kappaleen, jonka aika kulkee paljon hitaammin. Kun kappale saavuttaa valonnopeuden, se on nolla t-akselilla, mikä tarkoittaa, että se ei ole edennyt ajan suunnassa. Periaatteessa maailmaviivat osoittavat, että kun valonnopeus saavutetaan, aika pysähtyy havaitsijan kannalta. Maailmanviivoja käytetään hyvin usein teoreettisessa fysiikassa ja erityisessä suhteellisuusteoriassa sekä yleisessä suhteellisuusteoriassa.
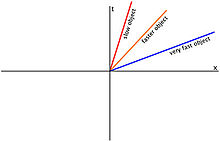
Kolmen eri nopeudella kulkevan kappaleen erilaiset reitit ja niiden mittaamat ajan kuluminen, jossa t-akseli edustaa ajan kulumista ja x-akseli kappaleen nopeutta.
Käyttö
Maailmaviivojen käsitettä käytetään laajalti teoreettisessa fysiikassa, sillä se osoittaa joitakin mielenkiintoisia tosiasioita nopeasta liikkeestä. Esimerkiksi Albert Einsteinin esittämä aikadilataatioyhtälö on algebrallisesti määrittelemätön, kun kappaleen nopeus on valonnopeus, mutta maailmaviivojen avulla voidaan todeta, että kun nopeus on valonnopeus, aika pysähtyy. Vaikka Einsteinin yhtälö (aikadilataatiolle) osoittaa, että valoa nopeammin kulkeva kappale kulkee ajassa taaksepäin, sama käsite voidaan kuvata käyttämällä maailmaviivoja.
| Osa artikkelisarjasta, joka käsittelee | ||||||
| Yleinen suhteellisuusteoria | ||||||
|
| ||||||
| ·
·
| ||||||
| Peruskäsitteet
| ||||||
| Ilmiöt
| ||||||
| ||||||
| Ratkaisut
| ||||||
Kysymyksiä ja vastauksia
Q: Mikä on maailmanraja?
A: Maailmanympärysviiva on ainutkertainen reitti, jonka kohde kulkee kulkiessaan sekä avaruudessa että ajassa, jota yleensä kutsutaan avaruusajaksi.
K: Miten erityinen suhteellisuusteoria selittää, miten aika kuluu eri nopeuksilla kulkeville kappaleille?
V: Erityisen suhteellisuusteorian mukaan aika hidastuu sitä enemmän, mitä nopeammin kappale kulkee. Hitaamman kappaleen aika kuluu nopeammin kuin hyvin nopean kappaleen, mikä tarkoittaa, että aika kuluu niille paljon hitaammin.
K: Mitä tapahtuu, kun esine saavuttaa valonnopeuden?
V: Kun kappale saavuttaa valonnopeuden, sen t-akseli on nolla, mikä tarkoittaa, että se ei ole edennyt ajan suunnassa. Tämä tarkoittaa, että aika pysähtyy havaitsijan kannalta.
Kysymys: Millä alueilla käytetään maailmaviivoja?
V: Maailmanviivoja käytetään hyvin usein teoreettisessa fysiikassa ja erityisessä suhteellisuusteoriassa sekä yleisessä suhteellisuusteoriassa.
K: Miten voimme visualisoida maailmaviivan?
V: Voimme havainnollistaa maailmaviivaa tarkastelemalla kuvia, jotka osoittavat, miten eri nopeuksilla kulkevat kappaleet kokevat ajan kuluvan eri nopeudella.
K: Voiko maailmaviivaa muuttaa tai muuttaa millään tavalla, kun se on kerran luotu?
V: Kun maailmaviiva on kerran muodostettu, sitä ei voi muuttaa tai muuttaa, koska se edustaa muuttumatonta polkua avaruusajan läpi.
K: Mitä "t-akselilla" tarkoitetaan valonnopeuden saavuttamisen yhteydessä? V: "t-akseli" viittaa edistymiseen ajan suhteen - kun kohde saavuttaa valonnopeuden, sen edistyminen ajan suhteen on nolla tällä akselilla, mikä tarkoittaa, ettei edistymistä ole tapahtunut avaruusajan läpi kulkemisen suhteen.
