Mikä on gravitaatiolinssi? Selitys, esimerkit ja vaikutus
Tutustu gravitaatiolinssiin: selkeä selitys, havainnolliset esimerkit ja vaikutukset — miten galaksit ja mustat aukot taittavat valoa ja luovat kaksoiskuvat.
Gravitaatiolinssi johtuu siitä, että kaukaisen kohteen ja meidän välissä on massiivinen kappale. Se voi luoda vaikutelman kahdesta tai useammasta kohteesta, vaikka todellisuudessa niitä on vain yksi. Kohteen valo taittuu välissä olevan massiivisen kappaleen ympärille.
Massiivinen kappale, kuten galaksi tai musta aukko, luo avaruuteen erittäin voimakkaan gravitaatiokentän. Vaikutuksen tarkka luonne riippuu:
- Massasta: suurempi massa aiheuttaa voimakkaamman taipumisen ja suuremman suurennuksen.
- Etäisyyksistä: suhteet havaitsijan, linssin ja kaukaisen lähteen välillä vaikuttavat siihen, millainen kuva muodostuu.
- Tarkasta kohdistumisesta (alignment): mitä lähemmäs täydellistä suoraa linjaa lähde–linssi–havaitsija osuvat, sitä symmetrisempiä rakenteita (esim. Einsteinin rengas) voidaan nähdä.
- Massan jakaumasta: onko massa pisteen kaltainen, jakautunut galaksin keskukseen vai laaja galaksiryhmän/klusterin tasolla — tämä muuttaa kuvan muotoa (kaksoiskuvat, kaaret, renkaat).
Miten linssi toimii (lyhyesti)
Yleisessä suhteellisuusteoriassa massa kaareuttaa aika-avaruuden. Valonsäde kulkee tätä kaarevaa avaruutta pitkin, jolloin sen suunta näyttää muuttuvan — käytännössä havaitsija näkee lähteestä tulevan valon näyttäytyvän eri paikassa kuin missä lähde todellisuudessa on. Erottelua kuvaa usein joko voimakas linssivaikutus (strong lensing), jolloin nähdään selkeitä useita kuvia tai renkaiden ja kaarien muodossa, heikko linssivaikutus (weak lensing), joka näkyy pienten muotojen/systemaattisten venymien tilastollisena vinoutumana, tai mikrolinssi, jossa pieni kohde (esim. tähti tai planeetta) aiheuttaa hetkellisen kirkkauden nousun kaukaisemman kohteen valossa.
Esimerkkejä ja havainnot
- Einsteinin rengas: lähes täydellisessä kohdistuksessa lähde muodostaa ympyrän muotoisen renkaan linssin ympärille.
- Moninkertaiset kuvat: sama kaukainen kvasaari tai galaksi voi näkyä useana erillisenä kuvana (esim. tunnettu "Einstein Cross").
- Kaaret galaksiklustereissa: massiiviset klusterit muodostavat pitkiä kaaria ja venyneitä kuvia taustagalakseista.
- Mikrolinssi-ilmiöt: tähtien tai planeettojen havaitseminen kirkkauden lyhytaikaisina vaihteluina; käytetty mm. eksoplaneettojen etsintään (OGE L-tyyppiset havainnot).
Tieteelliset ja käytännön merkitykset
- Massan ja pimeän aineen kartoitus: linssivaikutuksia analysoimalla voidaan päätellä linssin massajakauma myös silloin, kun massa ei säteile (pimeä aine).
- Kaukaisten kohteiden suurennus: gravitaatiolinssit toimivat "luupeina", joiden avulla voidaan havaita erittäin himmeitä, kaukaisia galakseja ja tutkia varhaista maailmankaikkeutta.
- Aikaviiveet ja kosmologiset mittaukset: monen kuvan välillä mitatut valon kulkuajan erot voidaan käyttää Hubble- vakion (H0) arvioimiseen.
- Ekso- ja substellar-tutkimus: mikrolinssit ovat auttaneet löytämään eksoplaneettoja ja rajaamaan mahdollisia pöly- tai kompaktien kohteiden tiheyksiä (MACHO-tutkimukset).
Yksinkertainen laskennallinen kuvaus
Alkeistasolla valon taipuma pienellä kulmalla voidaan esittää likimäärin deflektio- kulmana α ≈ 4GM/(c^2 b), missä G on gravitaatiovakio, M linssin massa, c valonnopeus ja b lähettimen pienin etäisyys (impact parameter). Käytännössä havaintojen tulkintaan käytetään linssiyhtälöitä ja numeerisia malleja, jotka ottavat huomioon massanjakauman ja geometriset etäisyydet.
Mitä kannattaa huomata
- Gravitaatiolinssi ei luo uutta valoa — se vain muuttaa ja suurentaa olemassa olevaa valoa.
- Ilmiö toimii kaikilla aallonpituuksilla, mutta havaintotekniikat (optinen, radio, röntgen) tuovat esiin eri yksityiskohtia dependin linssin massasta ja koostumuksesta.
- Usein linssidatan tulkinta vaatii malleja ja tilastollista analyysiä, koska samankaltaiset kuviot voivat syntyä eri massajakaumilla ja eri etäisyyksillä.
Yhteenvetona: gravitaatiolinssi on voimakas työkalu kosmologiassa ja tähtitieteessä — se paljastaa massan jakautumisen (myös pimeän aineen), suurentaa kaukaisia kohteita ja antaa mahdollisuuden mittailla kosmologisia parametreja, joita muuten olisi vaikea tavoittaa.

Einsteinin risti: neljä kuvaa yhdestä kvasaarista
Einstein
| Osa artikkelisarjasta, joka käsittelee | ||||||
| Yleinen suhteellisuusteoria | ||||||
|
G μ ν + Λ g μ ν = 8 π G c 4 T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }} | ||||||
| ·
·
| ||||||
| Peruskäsitteet
| ||||||
| Ilmiöt
| ||||||
| ||||||
| Ratkaisut
| ||||||
| · v · t · e |
Albert Einstein ennusti gravitaatiolinssien mahdollisuuden. Havainto, että aurinkomme taivuttaa kaukana olevien kohteiden valoa, kun niiden valo kulkee sen läheltä, oli todiste siitä, että yleinen suhteellisuusteoria oli oikea.
Linssien tyypit
Linssejä on kolmea eri tyyppiä:
- voimakas linssi
- heikko linssi
- microlensing
Voimakas linssi
Voimakas linssihavainnointi paljastaa itsensä tuottamalla useita kuvia samasta kohteesta. Tunnettu esimerkki on Einsteinin risti (Q2237+0305) 8 miljardin valovuoden päässä. Tässä tapauksessa gravitaatiolinssi tuottaa neljä kuvaa samasta kohteesta (kvasaari), vaikka se on vain yksi kohde. Kvasaarin valo ei kulje suoraviivaisesti Maahan. Sen sijaan se taipuu sen edessä olevan galaksin gravitaatiokentän mukaan. Tämä galaksi on 400 miljoonan valovuoden päässä.
Ensimmäinen tällainen löytö (Aurinkoa lukuun ottamatta) tehtiin vuonna 1979. Kaksi kvasaaria oli lähellä toisiaan. Molemmilla oli sama spektri, ja ne osoittautuivat saman kvasaarin (Q0957+651) kahdeksi kuvaksi. Vuonna 1980 tutkijat saivat selville, mikä galaksijoukko toimi linssinä.
Heikko linssi
Heikko linssi ei tuota useita kuvia samasta kohteesta. Sen sijaan se tuottaa erittäin epämuodostuneen tai venytetyn kuvan kohteesta, joka on kaukana linssin takana. Vuonna 1986 tämä havaittiin Abell 370 -joukossa. Myöhemmin ymmärrettiin, että kyseessä oli voimakkaasti deformoitunut kuva galaksista, joka oli kaukana ryppään ulkopuolella.
Kohde voi näyttää suuremmalta tai pienemmältä, kuten taulukossa on esitetty. Heikkojen linssien avulla voimme havaita hyvin kaukaisia galakseja, joita emme pystyisi havaitsemaan ilman tällaista linssiä. Taivuttamalla valoa valonlähteestä tulevan valon määrä (magnitudi) kasvaa. Näin hyvin kaukaisesta ja heikosta galaksista voi tulla näkyvä, vaikka normaalisti emme pystyisi havaitsemaan sitä.
Mikrolisensointi
Mikrolisenssitapauksissa muoto ei vääristy. Kohteesta näkyvän valon määrä muuttuu kuitenkin jaksoittain. Tätä voidaan käyttää eksoplaneettojen havaitsemiseen. Lähempänä olevan tähden painovoimakenttä taivuttaa ja voimistaa kaukaisen tähden valoa. Lähempänä olevan tähden ympärillä pyörivän eksoplaneetan läsnäolo taivuttaa kauempana olevan tähden valoa jaksoittain. Kohde OGLE-2005-BLG-390-Lb, joka löydettiin 25. tammikuuta 2006, on ensimmäinen mikrolisäyksen avulla havaittu eksoplaneetta.
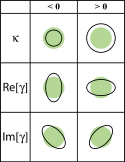
Vääristymät.
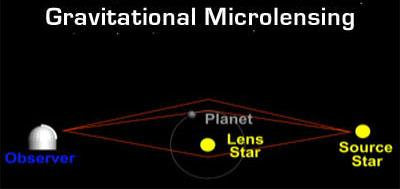
Eksoplaneetan löytäminen kaukaisen tähden valon avulla.
Etsiä

